

|
Astronomy 161:
An Introduction to Solar System Astronomy
Prof. Richard Pogge, MTWThF 2:30
|
Lecture 21: Dance of the Planets
Key Ideas
Every object in the Solar System feels gravitational pulls from
all of the other objects in the Solar System.
The Three-Body Problem
- Lagrange Points
- Examples: Earth-Moon and Sun-Jupiter systems
Gravitational Interactions
- Long-range Perturbations (discovery of Neptune)
- Close Encounters (slingshot effect)
Resonances
- Orbital (Mean-Motion) Resonances
Beyond Kepler
Newton's formulation of
Kepler's Laws of Planetary
Motion is only strictly true for idealized systems with only 2
massive bodies.
But, the Solar System is a many-body system:
- 8 Planets
- Multiple Moon Systems around 6 planets
- Millions of small Asteroids and Icy Bodies
- Lots more smaller debris (meteors & comets)
How do we address this many-body problem?
The Three-Body Problem
Let's start relatively simple:
What is the orbit of a small body in the combined gravitaional
field of two larger objects orbiting each other?
Some examples:
- Spacecraft in the Earth-Moon system
- An asteroid orbiting the Sun near Jupiter
A formal solution of the problem was proposed by French mathematician
and physicist Joseph-Louis Lagrange (1736-1813)
- Solved the "Restricted 3-Body Problem", in which the third body has
a negligible mass compared to two more massive bodies in circular orbits around
their common center of mass.
- Found 5 "islands of equilibrium" that orbit in lock-step with the
two main bodies.
These are known as the Lagrange Points, labelled L1
through L5.
Earth-Moon Lagrange Points
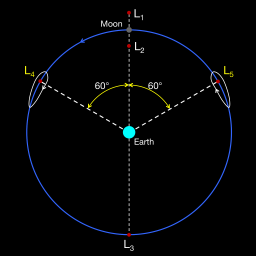
- Earth-Moon Lagrange Points
- L4 and L5 are stable:
- Can have objects trapped in stable "tadpole" orbits.
- L1 through L3 are unstable:
- Objects at these points are easily nudged out of their orbits
and drift away (no long-term orbits without special circumstances, like
firing engines for "station-keeping maneuvers").
[21.1]
Jupiter Trojan Asteroids
An example of objects trapped in stable orbits at the L4 and
L5 Lagrange points are the Trojan Asteroids of Jupiter.
These are two families of asteroids that that follow and lead Jupiter
around the Sun as part of the Sun-Jupiter system.
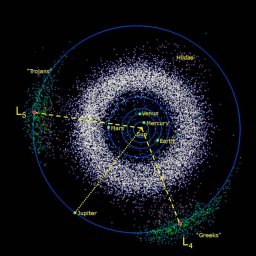
- Jupiter Trojan Asteroids.
Gravitational Interactions
To a first approximation, the orbits of most objects around the Sun are
simple 2-body Keplerian orbits:
- The Sun is ~1000x more massive than all of the planets, moons, and
small bodies combined.
- The Solar System (today) is mostly empty, with large distances
between big objects.
Since the Gravitational Force gets
weaker as the inverse square of the distance between objects:
- Gravitational pulls from the other bodies are typically small compared
to the Sun's gravity.
- But, they can accumulate over time...
- or, they can be strong if there are chance close encounters.
Long-Range Perturbations
Long-range interactions between two massive bodies orbiting the Sun.
The extra object-to-object gravitational forces accelerate the bodies
relative to their Keplerian orbits
- The orbits are perturbed from simple Keplieran paths
- Effect is strongest with the two objects are lined up at opposition
(closest approach to each other).
- Less massive objects are accelerated more.
- The perturbations can accumulate over time, though generally
they mostly cancel out.
Any systematic deviation of a body's orbit from a simple Keplerian
path is usually a sign that the body is being perturbed by the gravity
of another, nearby object.
The Discrepant Orbit of Uranus
William Herschel accidentally discovered the planet Uranus in 1781 while
sweeping the sky with his telescope in his backyard in Bath, England.
Uranus is the 7th planet, orbiting beyond Saturn.
Subsequent measurements of the orbit of Uranus started showing
systematic discrepancies between the predicted and actual positions of
Uranus in the sky. By the 1840s, these discrepancies had become as
large as 1 arcminute!
- Uranus was accelerating in its orbit because of the combined
gravity of other massive objects in the Solar System.
The problem was, if you added up the perturbations from the known planets,
it wasn't enough to explain the discrepancy seen.
- Extra acceleration was from the gravity of an 8th, as yet unknown
massive planet orbiting somewhere beyond Saturn!
The Discovery of Neptune
Two theorists, Urban LeVerrier in France and John Couch Adams in
England, predicted that the deviations were due to the gravitational
influence of another, unknown massive planet beyond Uranus.
Using the deviant motions of Uranus, they independently
calculated where this unknown 8th planet should be.
- Adams was ignored by English astronomers.
- Leverrier convinced Galle in Berlin to search.
On Sept 23 1846, Galle found Neptune only 52 arcminutes from where
Leverrier predicted it would be!
This was possible because between Uranus' discovery in 1781 and the
1840s, Neptune passed through opposition with Uranus, when the
perturbation of Uranus by Neptune's gravity is strongest. If their
configuration had been conjunction, there would not have had a
measurable perturbation. Neptune would have eventually been discovered
by accident like Uranus, in fact Galileo saw it while observing
Jupiter but thought it was a fixed star!
[21.2]
Close Encounters
Close encounters between objects have much stronger effects:
- They can dramatically alter the orbits of one or both bodies.
- Smaller objects are more strongly affected by close
encounters with larger bodies.
Examples:
- Short Period Comets
- An incoming comet on a large elliptical or near-parabolic orbit with
a very long period is driven into a smaller elliptical orbit with a
shorter period after a close gravitational encounter with Jupiter.
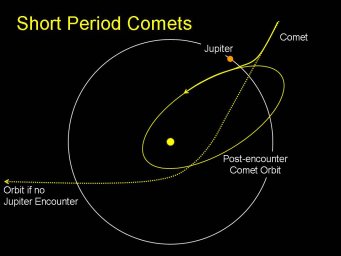
- The dashed path is the orbit the comet would follow if it had no
Jupiter encounter.
- The solid line show the new, smaller ellitpical comet orbit after a
close gravitational encounter with Jupiter,
- Gravitational Slingshot
- A spacecraft catches up with Jupiter from behind, and is accelerated
by Jupiter's strong gravity. This, combined with Jupiter's orbital motion,
give the spacecraft a boost in speed, slinging it into the outer
solar system.
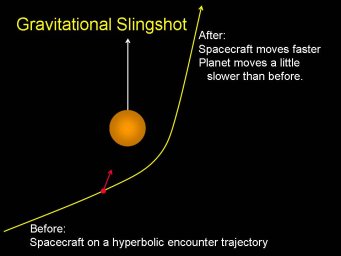
- This method of "gravity assist" is used to send spacecraft into
the outer Solar System by robbing Jupiter of a tiny bit of its orbital
energy. This is much more energy efficient than having to carry a very
heavy payload of fuel to rocket the spacecraft to those speeds.
- This was done by all outer Solar System explorers (Voyager 1 & 2,
Pioneer 10 & 11, Cassini, and New Horizons).
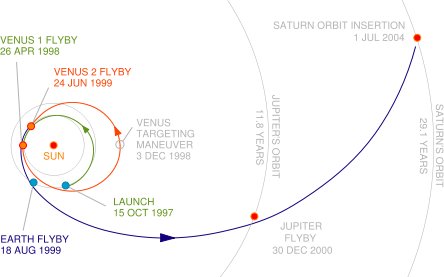
- Above is the Cassini gravity assist trajector to Saturn. Boosts
from Venus, Earth, and Jupiter were used to get Cassini to Saturn with
minimal expenditure of fuel (and so less spacecraft weight).
- The reverse process, where the encounter occurs with the spacecraft
getting in front of the planet, can be used to take energy from the
spacecraft, dropping it deeper into the inner Solar System. This is
done for spacecraft bound for Mercury like MESSENGER.
Small perturbations at opposition usuall happen at different places along the
object's orbit.
- The combined effects tend to average out over long times.
But, if the periods of the object and its perturber are whole-number
ratios, you can get regular, periodic pertubations at the same place
in the orbit.
- The repeated accelerations add up over time and amplify.
- If there are regular close encounters, the smaller object
can get destablized over time and cleared out of its original
orbit.
- If the synchronization avoids close encounters, the orbit can be
stabilized.
We say that such synchronized pairs of orbits are Orbital
Resonances.
The analogy is to consider a child on a swing being pushed another
person:
- If the pushes of the child come at random times, sometimes pushing
with their swing and boosting them, other times pushing against their
swing and slowing them down, they average out and the swing doesn't
change much.
- However, if the pushes are all timed just right so that you push the
child with their swing each time, the in-phase pushes build up and the
child's swing gets amplified.
- Such a well-timed push is called exciting a resonance.
Orbital resonances are a way to amplify small long-range
gravitational perturbations.
Naming Resonances
Resonances are named for the number of orbits completed by each body in
the pair.
- The first number is the number of orbits completed by body being
most perturbed.
- The second number is the number of orbits completed in the same time
by the perturber
Examples:
- Pluto is in a 2:3 Resonance with Neptune
- Pluto completes 2 orbits for every 3 orbits of Neptune.
- Pluto is the smaller object being driven by Neptune.
- Asteroid Hilda is in a 3:2 Resonance with Jupiter
- Hilda completes 3 orbits for every 2 orbits of Jupiter.
- Hilda is the smaller object being driven by Jupiter.
Resonances in the Solar System
Some examples of important orbital resonances in the Solar System:
- Main Asteroid Belt Resonances with Jupiter
- Kirkwood Gaps - unstable resonances cleared of asteroids
- Asteroid Families - stables resonances populated with asteroids
orbiting with the same periods.
- Trojan Asteroids - 1:1 resonance with Jupiter
- Kuiper Belt Resonances with Neptune
- Pluto and the Plutinos in 2:3 resonance orbits
- Twotinos - objects in 1:2 resonance orbits
- Jupiter and Saturn Systems
- Jupiter: 1:2:4 Laplace Resonance of the moons Io, Europa, and Ganymede
- Saturn: many resonant moons and resonant gaps in the rings.
We will meet each of these as we begin our exploration of the Solar
System in upcoming lectures.
Dynamical Evolution (again)
The Solar System is not a "static" clockwork that moves exactly the same
forever
- The dynamical state of the Solar System changes over time as the
planets interact via their mutual gravitation.
Close Encounters and Resonances amplify these changes:
- Close encounters re-arrange orbits, and can even kick small bodies
out of the Solar System.
- Some resonances destabilize small-body orbits, depopulating some orbits
(Kirkwood Gaps in the Asteroids, Ring Gaps around Saturn)
- Some resonances are stable, and objects swept into them can form
distinct dynamical "families" of objects.
All of these effects have helped "shape" the Solar System over its long
history.
As we explore the Solar System in more detail later in the course, we will
keep on the lookout for signs of this "dynamical evolution", and use it to
help read the dynamical history of the Solar System.
Return to [
Unit 4 Index
|
Astronomy 161 Main Page
]
Updated: 2016 March 30
Copyright © Richard W. Pogge,
All Rights Reserved.




