

|
Astronomy 161:
An Introduction to Solar System Astronomy
Prof. Richard Pogge, MTWThF 9:30
|
Lecture 21: The Rotation & Revolution of the Earth
Key Ideas:
Demonstrations of the Earth's Rotation about its axis:
- Coriolis Effect
- Foucault Pendulum
Demonstration of the Earth's Revolution around
the Sun:
Eppur si muove (?)
Legend has it that Galileo muttered the words "Eppur si muove" (It
still moves) under his breathe after abjuring his "errors and heresies"
before the Roman Inquisition in thew matter of teaching the forbidden
Copernican system.
This story is almost certainly false, but it touches upon
the principal objection to the Heliocentric System since the
time of Aristotle:
How do you prove that the Earth really does rotate upon its axis and
revolve around the Sun?
The Need for Speed
A major conceptual barrier to accepting the rotation and revolution
of the Earth is that the speeds required are enormous.
- Speed of the Earth's Rotation at the Equator:
- Circumference of the Earth at the Equator = 40,000 kilometers
- Time to complete one Rotation = 24 hours
- Speed of Rotation = Distance/Time = 40,000 km / 24 hr = 1670 km/hr
The speed of revolution around the Sun is even larger:
- Speed of the Earth's Revolution around the Sun:
- Radius of the Earth's Orbit = 1 AU = 150,000,000 kilometers
- Circumference of the Earth's Orbit = 2*pi*R = 942,000,000 kilometers
- Time to complete one Orbit = 365.2422 days = 8766 hr
- Speed of Revolution = Distance/Time = 942,000,000 km / 8766 hr = 107,000 km/hr = 30 km/sec
In the typical time it takes to read this sentence (about 15
seconds), the Earth will have moved through space by about 450 km, or
about the width of the state of Ohio.
Consider that the fastest things people had experienced prior to
the invention of steam power moved at speeds of only a few 10s of km/hr
(horses, fast ships). Even the fastest winds are only 150 km/hr.
Riding on a Rotating Sphere
As you move north or south of the equator towards the Poles:
- East-West parallel of constant latitude narrows.
- The distance covered in 24-hours is less, so the speed
is less.
The speed of rotation is greatest at the Equator and gets
smaller with increasing latitude.
For example, at Columbus (Latitude 40-degrees North):
- Circumference of the Earth at 40-deg North = 30,600 kilometers
- Time to complete one Rotation = 24 hours
- Speed of Rotation at 40 North = Distance/Time = 30,600 km / 24 hr = 1280 km/hr
[Note: For the more mathematically inclined, the rotation speed at a
given Latitude = cos(Latitude) x 1670 km/hr.]
The Coriolis Effect
First described by French physicist Gustave Coriolis in 1835.
Deflection of a projectile due to the Earth's Rotation:
An example:
- Fire a cannonball due North from a cannon on the Equator.
- The cannon is moving east with the Earth's rotation
at a speed of 1670 km/hr.
- The cannonball retains its initial, faster, eastward speed
as it flies north (Newton's First Law).
- The further north it flies, the slower the eastward motion
of the Earth's surface beneath its flight.
Result is a slight eastward deflection of the cannonball from
its original northward trajectory. You get the same effect if you fire
the cannon towards the South.
The above is a simple illustration of the Coriolis effect. In
general, the Coriolis effect works independently of the direction in
which the projectile is travelling.
A Little to the Right (or Left)
The result of the Coriolis Effect is:
- Projectiles are deflected towards the right at northern latitudes.
- Projectiles are deflected towards the left at southern latitudes.
Modern long-range artillery fire-control and missile guidance systems
are designed to correct for the Coriolis Effect.
Also affects low-pressure systems & storms:
- Hurricanes in the Northern Hemisphere rotate Counter-Clockwise
- Tropical Cyclones in the Southern Hemisphere rotate Clockwise
Flushing an Urban Legend
The Coriolis Effect does not cause water to spiral down drains (or
toilets) differently in the Northern & Southern Hemispheres.
- The size of a sink, tub, or toilet bowl is too small compared to the
size of the Earth.
- Coriolis Effect is much smaller than other motions, like water jets
or swirling the water with your hand.
Try it: Fill a sink with water, set the water it swirling
clockwise and then pull the plug. Then do it again, this time swirling
it counterclockwise before pulling the plug. The direction of rotation
of a draining sink or toilet is determined by the sense of rotation of
disturbances in the water (as above), or the sense of rotation imposed
when the basin was filled, etc., but not by the Coriolis force.
Sorry Bart (the clockwise flush fallacy was the premise of the
Bart
vs. Australia episode of The Simpsons).
Another likely-sounding but utlimately fallacious Coriolis Force myth is
set during the First World War at the Battle of the Falklands between
British and German naval forces in the South Atlantic. The story goes
that early in the battle, British shells kept falling consistently about
100 meters to the left of the German ships because the gunners neglected
to take into account the opposite sign of the Coriolis effect in the
Southern hemisphere (most of their experience was in the North), and so
they were inadvertently correcting for the Coriolis effect in the wrong
direction, resulting in twice the deflection that would occur if no
correction had been made! While this story has made it into at least
one physics textbook that I used back in the 1980s, and is now a
common-place on the Internet, I've have never yet read an account of
this story in historical accounts of the Battle of the Falklands, which
was an important engagement and much discussed. A straightforward
calculation, beyond the scope of this introductory course, readily shows
that this is a bit of physics mythology.
Foucault Pendulum
Built by Jean Foucault in 1851. He suspended a 67-meter long pendulum
with a 25-kg weight from the dome of the Pantheon in Paris. A
ball joint let the pendulum swing freely in all directions.
- Started the pendulum swinging North-South.
- A few hours later, it was swinging NorthEast-SouthWest.
- Later still it was swinging East-West.
- and so forth...
The steady clockwise shift of the pendulum's swing is being caused
by the rotation of the Earth.
The Pole and the Pendulum
The easiest way to see what is going on is to imagine erecting
a Foucault Pendulum at the North Pole.
Start the pendulum swinging towards the direction of a particular
star (e.g., the bright star Sirius).
An observer on Sirius looking at the pendulum would see:
- Direction of the pendulum's swing is constant (always towards Sirius).
- Earth rotates counterclockwise every 24 hours.
An observer at the North Pole would see:
- Earth doesn't rotate relative to the observer (you see the Earth
stationary beneath your feet).
- The pendulum's swing rotates clockwise once every 24 hours.
What is rotating (the Earth or the Pendulum) depends on your point of
view.
At middle latitudes, a Foucault pendulum takes longer than 24 hours
to go around once [more exactly, it takes 24hr x sin(latitude), so in
Columbus, it takes 37.3 hours. Foucault pendulums don't swing around at
the Equator].
If the earth were not rotating, the pendulum would never change the
direction of its swing at any latitude above the Equator.
Stellar Parallax
As the Earth revolves around the Sun, it moves 2 AU from one side of
its orbit to another in 6 months.
- Viewed from these two different locations, a nearby star would appear
to shift position with respect to more distant stars.
- The amount of the shift is called the "Stellar Parallax".
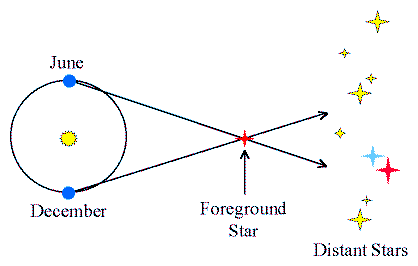
(Click on the image to view at full scale [Size: 7Kb])
Parallaxes were not observed at the time of Copernicus:
- The "non-observation of stellar parallaxes" was one of the principal
objections to the Copernican heliocentric model.
- Copernicus and others countered that this was because the stars
were too far away to produce measurable parallaxes.
Parallax decreases with Distance
As the distance to a star increases, the amount of parallax
decreases. This is easy to see in the following two figures:
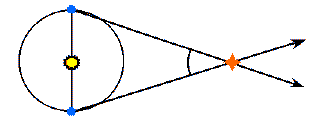

In the upper figure, the star is about 2.5 times nearer than the star
in the lower figure, and has a parallax angle which is 2.5 times
larger.
A movie demonstrating
parallaxes is available (beware: it is big, don't try to download it over a
slow modem link).
Measuring Stellar Parallaxes
Copernicus and others were right: stellar parallaxes were not easily
observed because the stars are much more distant than people originally
suspected:
- All stellar parallaxes are less than 1-arcsecond
- The nearest star with the largest parallax is Alpha Centauri,
with a parallax of 0.76 arcsec.
- Such small angles cannot be measured using naked-eye techniques
(e.g., the best measurements by Tycho Brahe were 1-2 arcminutes,
or about 100x larger than the largest parallax).
The first stellar parallax was observed in 1837 by the astronomer
Friedrich Wilhelm Bessel for the star 61 Cygni.
- Used a telescope to make the measurements.
- Measured a parallax of about 0.3 arcsec.
- Corresponds to a distance of ~10 light years for 61 Cygni.
- Notes:
- Modern measurements of parallaxes use photography or digital imaging
techniques. A new generation of "interferometric" techniques is being
developed for upcoming space missions that will be able to measure
parallaxes with a precision of 1 microarcsecond.
- As you will learn in Astronomy 162, stellar parallaxes provide us
with an important method for making direct measurements of the distances
to planets and nearby stars.
- The revolution of the earth was first demonstrated not by
parallaxes but by the discovery of the "aberration of starlight" by the
astronomer James Bradley in 1728. Parallaxes, the "final proof", were to
be elusive for more than a century, and were one of the chief goals of
astronomers in this period.
Cosmic Anticlimax
Firm observational proof of the rotation and revolution of the Earth
did not come until more than two centuries after the death of
Copernicus.
By then, the use of the telescope and the revolution in thought
started by Isaac Newton's formulation of the laws of motion and
gravitation had effectively swept away the last vestiges of the
Aristotelian view of the world.
Return to [
Unit 4 Index
|
Astronomy 161 Main Page
]
Updated: 2006 October 14
Copyright © Richard W. Pogge,
All Rights Reserved.


