The Heights of Lunar Craters

Please read the "Laboratory Rules of Operation" before proceeding.
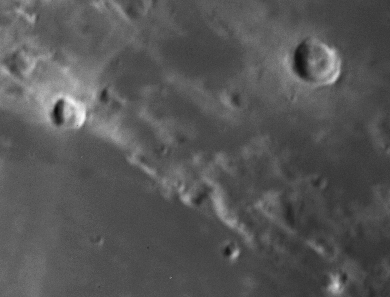
This lab is based on an unfiltered CCD image of craters near the center of the first-quarter moon that were acquired with a SpectraSource Instruments Teleris CCD camera on the old 12-inch Tinsley telescope that used to reside in the dome on the roof of Smith Lab. The images were taken on 1998 September 28 EDT.
The Teleris camera uses a Kodak KAF-0400 768x512 CCD with 9-micron pixels. The Tinsley reflector was a 12-inch (0.305-meter) aperture telescope with an f/16 cassegrain focus. The CCD was roughly aligned with its long axis oriented along the East-West direction in the sky, and the short axis North-South. Both zero (bias) and flat-field calibration images were also acquired. Because the integration times are so short, no dark images were required.
Because we are viewing these craters just after dawn from their point of view, the crater walls cast long shadows. Using a simple geometric technique pioneered by Galileo Galilei in 1610, we can estimate the physical heights of the crater walls. Along the way we'll learn some basic image processing techniques.
Goals
The goals of this lab are as follows:
This lab will make use of the Linux workstations in MP4042 and the XVista image processing package. You will also need to use an Internet browser to search some online catalogs for information (either your own PC or one of the Windows PCs in MP4042), and you will need to use the reading room to consult copies of the various Lunar Atlases and The Astronomical Almanac for 1998.
[Index]
Login to one of the Linux workstations in MP4042. For this guide, I will denote Unix commands by a "%", which is the generic Unix command prompt. Commands in this guide given without a % are XVista commands (i.e., issued in response to the XVista "GO" prompt).
For this part, do the following:
% cp /home/regulus/ast350/LabData/MoonLab/moon98.fits .
If you type this command again, it will replace your
working copies with new copies (and wipe out the old ones). It
copies one (1) files into your working directory:
moon98.fits, a pre-processed FITS-format image of
the moon described above.
% xvista
once you get the XVista command prompt (GO:), you
are ready to begin. For details on basic XVista
commands, see the Vista Tutorial and Cookbook
in the white binder in the lab workstation area.
Extract Basic Image Information
Now that you have a reduced moon image to work with, you need to derive some basic information about this image. This includes
abx 1 alland read the output on the screen. Answer the following:
histogram 1 xmin=100 xmax=1523 nolog
which will plot the histogram of pixel data values. Add the
hard command to the line above to make a hardcopy and
add this to your notes. Answer the following questions:
impost 1 z=0 l=100 scale=0.54 file=mycrater.ps positive
This will create a PostScript file with your image in the file
mycrater.ps in your working directory. You should
replace "mycrater" with your lastname, just so we know whose file
it is. The positive keyword ensures that the picture
comes out as a "positive" print.
To print the PostScript file from inside XVista use the command:
$ lpr mycrater.ps
(or whatever you called the print file). The default printer is the
laser printer in MP4042. As long as you are using the
ast350 lab account, this printer will be the default
printer (no guarantees for other accounts).
We are now ready for Part 2.
[Index]
Now you have to hunt down some information in the library or on the web:
Identify the Craters and other Features
The best resources for finding what part of the moon we are looking at are the Lunar Atlas and the Times Atlas of the Moon. The former is the large black book on the reserve shelf in the reading room, whereas the latter is a thinner volume put out by the New York Times during the Apollo Moon landings. Neither of these books is to leave the reading room. The relevant identification photographs in the Lunar Atlas are found on plates 24-35 (pages 62-85). Remembering the moon phase, and that the image is of a region near the dawn terminator should help narrow down your search. Also remember that the moon is on average about 1/2-degree across, and that our CCD image is fairly small by comparison (as you computed above). This should give you some idea of what fraction of the surface we are looking at. Identify all of the named craters, mountains, and maria in your image.
Find the Selenographic Coordinates of the Craters
Once you have located the field and identified the named craters (not all are in the Atlas), search the USGS Flagstaff Office website for the tables of Lunar Features (see under "Data and Software", then "Databases", then "Planetary Nomenclature", you follow the chain the rest of the way to a table of Lunar crater names. This gives a great table of the selenographic (lunar) latitudes and longitudes for all craters, as well as the diameter of the craters in kilometers, and other information that might be relevant or interesting.
"Seleno" is the genitive form applied to the moon, thus selenology is the lunar equivalent of terrestrial geology, etc. Hence, selenographic coordinates refer to a coordinate grid defined on the lunar surface.
Sun/Moon/Earth Configuration
Using the 1998 edition of The Astronomical Almanac look up the Ephemeris of Physical Observations of the moon to get the configuration of the Sun, Moon, and Earth (as seen from the Moon) at the time of our observation. You will need to interpolate the values in the table to our observation time (0113 UTC) on 1998 Sept 29 (UTC). For our observations, you need to get the following values from the table:
These data give us the critical viewing geometry for using the shadow lengths to estimate the heights of the crater walls.
Also look up values for the mean radius of the Earth and the Moon (in kilometers).
Annotated Image and Table
Annotate your hardcopy of the enhanced image with the names of the major craters, mountains and maria.
Compile a table of the craters you have identified, and give the data extracted from the sources described above. Also make an accompanying table of the date of observation and the sun/moon/earth configuration information that you derived from the sources above.
[Index]
Using XVista and your copy of the moon image, measure the lengths of the crater shadows for the two largest craters on your image. Your measurement should be in units of pixels. Do this as follows:
Make an estimate the uncertainties in your measurements, giving what assumptions you have made (think about what fraction of a pixel you can make measurements of the positions of features)..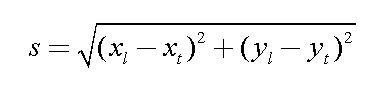
Remember to include your estimates of the uncertainties of these measurements.
[Index]
The geometry of a crater shadow is shown in the figure below:
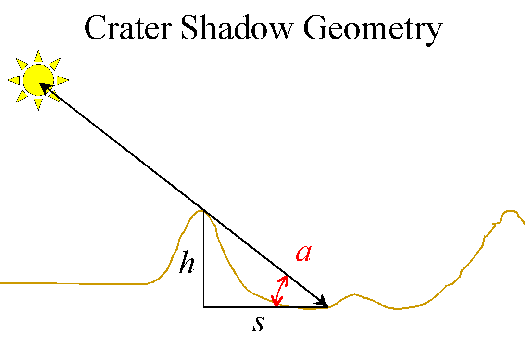
Fig. 1: Moon crater shadow geometry
The height of the crater is h, the apparent length of the shadow is s, and the altitude of the sun as seen from the end of the shadow is the angle a. They are related simply by:
From spherical geometry (you can derive it if you wish), the altitude of the sun as seen from a crater with selenographic latitude bc and longitude lc is given by: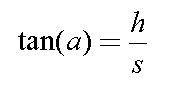
where bo and co are the selenographic latitude and co-longitude of the Sun, respectively.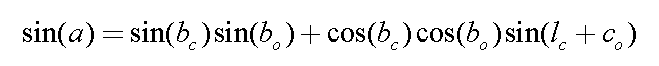
Using these formulae, your measurements, and the selenographic coordinates of the Sun and craters interpolated from the tables, estimate the heights of the crater walls, and their uncertainties.
[Index]
Whew! That was involved, huh?
The research you had to do to hunt down everything was relatively simple (i.e., because I told you where to look), and is similar to what you encounter in any scientific project. Making the actual measurements is only one part of the problem. Making sense of the measurements, like using them to estimate something interesting (like the heights of lunar crater walls), is quite another.
For your writeup, try to organize all these various steps into a coherent narrative. However, also keep it brief: be concise and to the point. I won't be impressed by lots of extraneous information or off-topic speculation. I will, however, wonder why you haven't stuck to the topic.
A typical outline would be:
This is not all that different than how one would organize observations, data analysis and interpretations into a scientific paper.
[Index]
An online catalog of lunar features, with selenographic coordinates and other data may be found at the website of the USGS Flagstaff Station in Flagstaff Arizona:
http://wwwflag.wr.usgs.gov/USGSFlag/Of other interest is a database of lunar images taken by the Clementine mission:
http://galilei.cmf.nrl.navy.mil/clementine/clib/featuresThis might help you identify the field, but trust me that you will find the annotated photographic Lunar Atlas prepared by the Space Sciences Laboratory of North American Aviation (1964) very useful. After you've identified the field, try the Times Atlas of the Moon for a more detailed set of topographic-style maps. There are other photographic atlases available (e.g., the moon atlas in the Norton's 2000.0), but I chose these because we have copies in our reading room and they were useful for this exercise.
Persons (other than Ast350 students who already have access to the data directly) are welcome to use the data and follow along with the lab. XVista is a publically available image processing package for Unix workstations (no Windows/NT/Mac ports planned), but any good image processing package that permits simple image arithmetic and smoothing operations will suffice. The trick is how to deal with the FITS image format.
The raw data consist of a single, unprocessed CCD image of the Moon acquired on 1998 Sept 29 01:13 (UTC) with the Teleris CCD camera on the 12-inch Tinsley Reflector on the roof of Smith Lab at OSU. A flat field and zero (bias) image were also acquired. This is the reduced, processed image:
[Index]
Copyright © Richard W. Pogge, All Rights Reserved.