Astronomy 162: Professor Barbara Ryden
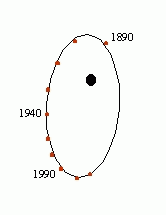
1) In a visual binary the stars appear
as two separate points of light. You can tell that they
are a binary system (instead of a chance alignment of
unrelated stars) by watching for a long period of time,
and seeing one star trace out an elliptical path relative
to the other, as shown below:

2) In a spectroscopic binary the stars are far enough away to appear blurred together into a single blob of light. However, by looking at the spectrum of the system, you can see the Doppler shift of the absorption lines change as the stars orbit the center of mass of the system. (This is the same method by which planets are discovered around other stars.)
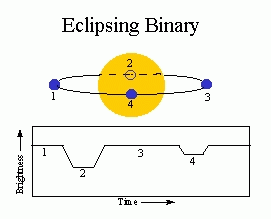
3) In an eclipsing binary the stars
are also far enough away to appear blurred together
into a single blob of light. However, if you are viewing
the stars' orbits nearly edge on (as shown below),
you will view periodic eclipses of
the stars. When the cool star is in front of the
hot star (position 2 below), there will be
a large drop in apparent brightness. When the hot
star is in front of the cool star (position 4),
there will be a smaller drop in brightness.
Armed with these methods of detecting binary systems, we can make a census of binary systems in the solar neighborhood. About 45 percent of stars are solitary, like the Sun. However, the remaining 55 percent are in binary systems, like Sirius A and Sirius B (some stars are even in triple or quadruple systems).
However, Isaac Newton modified Kepler's Third Law, so
that it applied to ANY pair of objects orbiting their
mutual center of mass. As modified by Newton, and applied
to a binary star system:
P2 ( M1 + M2 ) = a3 ,
where P = orbital period of stars (in years),
a = average separation of stars (in AU),
M1 = mass of 1st star (in solar masses), and
M2 = mass of 2nd star.
Thus, the total mass of a binary system can be found from the relation M1 + M2 = a3/P2 , as long as the values of a & P are known.
APPLICATION: Sirius A and Sirius B
Recall (from yesterday's lecture) that Sirius is actually a
binary system, consisting of a luminous main sequence star
(Sirius A) and a hot but dim white dwarf (Sirius B),
orbiting their center of mass.
The orbital period of the Sirius system is P = 50 years. (The
orbits of Sirius A and B have been tracked since the 19th century,
so their orbits are very well known.) The average separation
of Sirius A and Sirius B, taken over their entire orbit,
is a = 20 AU. (That's about the size of the orbit of Uranus.)
The total mass of the Sirius system is thus:
M1 + M2 = a3 / P2 =
8000/2500 = 3.2
Note that Kepler's Third Law only gives us the total mass of
the system. We now know that the mass of Sirius A and Sirius B,
taken together, is 3.2 Msun. We don't know whether the
two stars are equal in mass, or whether the more luminous star
(Sirius A) has the lion's share of the mass as well as the lion's
share of the luminosity.
Finding the mass of Sirius A and Sirius B individually involves
locating the center of mass of the Sirius
system. The center of mass of a binary system is its ``balance
point''; if you placed the two stars on the ends of a seesaw,
the center of mass is where you'd have to place the fulcrum
of the seesaw in order to make it balance. The center of mass
of a binary system is always closer to the more massive star.
The distances of the two stars from the center of mass is
given by the relation
M1 / M2 = a2 / a1 ,
where a1 = distance of 1st star from center of mass, and
a2 = distance of 2nd star from center of mass.
For example: observation of the Sirius system has revealed that
a1 / a2 = 0.45, where a1 is
the distance of Sirius A (the luminous main sequence star) from
the center of mass. Thus, the center of mass is closer to Sirius A
than to Sirius B; this tells us that Sirius A, the more luminous
star, is also the more massive star. In particular, we know that
M1 / M2 = a2 / a1 =
1 / 0.45 = 2.2
Thus, Sirius A is more than twice as massive as Sirius B.
We know that M1 + M2 = 3.2 Msun,
from Kepler's Third Law.
We know that M1 / M2 = 2.2, from the
location of the center of mass.
We deduce that the mass of Sirius A is M1 = 2.2 Msun,
and that the mass of Sirius B is M2 = 1 Msun.
For stars on the main sequence:
Stars more massive than the Sun are
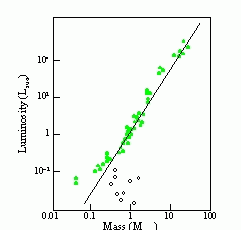
Objects with masses less than 0.08 Msun are too cool for fusion to occur in their cores; they are `brown dwarfs'. Stars with masses greater than 50 Msun don't seem to exist in significant numbers. (Question to ponder: Why not?)
What about stars off the main sequence? White dwarfs (such as Sirius B) are all roughly as massive as the Sun, but only as large as the Earth. This means that their densities must be *very* high.
Giants and supergiants do not have a simple mass-luminosity relation, the way main sequence stars do. (You can't make a good guess at a giant or supergiant's mass simply by knowing its luminosity.) However, the upper mass limit of 50 Msun applies to giants and supergiants as well as to main sequence stars. Thus, huge supergiants such as Betelgeuse, with a volume billions of times greater than the Sun's must be of very low density.
Betelgeuse isn't fat; it's just fluffy.
Updated: 2003 Jan 17
Copyright © 2003, Barbara Ryden