Astronomy 162: Professor Barbara Ryden
Monday, January 13
HOW FAR IS A STAR?
``How far would I travel
To be where you are?
How far is the journey
From here to a star?''
- Irving Berlin
Key Concepts
- Distances in the universe are important to know, but
difficult to measure.
- The distance to a nearby star can be found from its PARALLAX.
- On average, a nearby star will have a larger PROPER MOTION
than a distant star.
(1a) Distances in the universe are important to know.
Distances are required to compute:
- The luminosity of an object (a 25-watt bulb 50 meters away
appears just as bright as a 100-watt bulb 100 meters away).
- The size of an object (a large distant object [e.g. the
Sun] can be the same angular size as a small nearby object [e.g. the Moon])
- The mass of an object (this can be computed from Kepler's Third
Law if the object is part of an orbiting system).
(Besides, knowing the distance to a star is interesting in its
own right.)
(1b) Distances in the universe are difficult to measure.
It took a long time to measure distances to the nearest stars.
- Ptolemy [2nd century AD]: thought that all stars were at the
same (relatively short) distance, attached to a crystalline sphere
- Copernicus [16th century AD]: knew that stars were at a large
(but unknown) distance
- Friedrich Bessel [1838]: first person to measure the distance to a star other than
the Sun - used the method of stellar parallax
(2) The distance to a nearby star can be found from its parallax.
Definition: Parallax is the change in the apparent position of an object
which results from a change in the observer's position.
Simple example: Hold thumb at arm's length. Look first through one
eye, then through other. Thumb's position changes relative to background.
The closer your thumb to your eyes, the larger the jump in position.
More sophisticated example: Look at a star - first in June,
then in December, six months later.
Your location changes by 2 AU between these times. Therefore, the star's
position changes relative to more distant background
stars. The angle p (see the
diagram below) is the star's parallax.
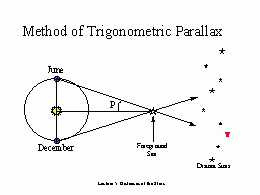
After measuring p, and knowing the size of the Earth's orbit,
we can compute the distance to the star using trigonometry.
Note that the distance to even the nearest stars (other
than the Sun) is much larger than 1 AU;
therefore, the angle p is small.
Measuring small angles:
- 360 degrees = full circle
- 60 arcminutes = 1 degree
- 60 arcseconds = 1 arcminute
Full circle = 360 X 60 X 60 = 1,296,000 arcseconds
1 arcsecond = angular size of dime 2 kilometers away
Important Equation: Computing a Distance from a Parallax
d = 1/p
d = distance to star, measured in parsecs
p = parallax, measured in arcseconds
The parsec is defined as the distance at
which a star has a parallax of 1 arcsecond. In other units,
1 parsec = 3.26 light years = 206,000 AU.
Parsecs are the units most often used by professional
astronomers in measuring interstellar distances.
Example:
The star Proxima Centauri has a parallax p = 0.77 arcsecond.
d = 1/0.77 = 1.30 parsec = 4.23 light years
Because stellar parallaxes are so small, they can
only be measured accurately for relatively nearby stars.
- From the ground, the smallest measurable parallax is p = 0.01 arcsec
(corresponding to a distance d = 100 parsecs = 326 light years).
- From a satellite, the smallest measurable parallax is
p = 0.002 arcsec (corresponding to a distance
d = 500 parsecs = 1600 light years).
For comparison, the distance from the Sun to the center of
our galaxy is about 8000 parsecs. Thus, we can only use the technique
of stellar parallax to measure distances in our immediate
neighborhood, not for the entire galaxy.
(3) On average, a nearby star will have a large proper motion.
Proper motion is the steady change in a star's
apparent position on the sky, resulting from its motion through space.
Proper motion is measured in arcseconds per year.
On average, close stars have faster proper motions than distant stars.
(This is only an average statement: a star which happens to be
moving directly toward or away from the Sun, for instance, will
have no proper motion.)
Examples:
- Proxima Centauri:
proper motion = 3.85 arcseconds/year, distance = 1.3 parsecs
- Betelgeuse:
proper motion = 0.03 arcseconds/year, distance = 150 parsecs
Searching for stars likely to be nearby? Look for stars with large
proper motion.
Prof. Barbara Ryden
(ryden@astronomy.ohio-state.edu)
Updated: 2003 Jan 13
Copyright © 2003, Barbara Ryden

