Astronomy 162: Professor Barbara Ryden

Monday, January 27

THE MAIN SEQUENCE

``Everything should be made as simple as possible - but not simpler.''
- Albert Einstein

Key Concepts

A main sequence star is powered by fusion of hydrogen into helium in its core.
Fusion is stabilized by a natural pressure-temperature thermostat.
High-mass main sequence stars have shorter lifetimes than low-mass main sequence stars.

(1) A main sequence star is powered by fusion of hydrogen into helium in its core.

Recall that a `Hertzsprung-Russell' diagram is a plot of the luminosity of stars versus their temperature. The main sequence on a Hertzsprung-Russell diagram is a diagonal band, running from cool, dim, small, low-mass stars (in the lower right corner) to hot, luminous, big, high-mass stars (in the upper right corner):

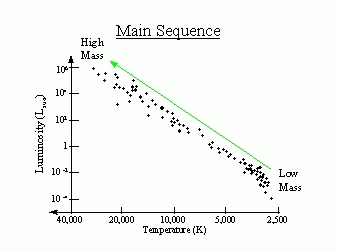
All main sequence stars (including the Sun) are powered by the fusion of hydrogen (H) into helium (He). Fusion of hydrogen requires temperatures of more than 10 million Kelvin. Above this temperature, the fusion rate is strongly dependent on temperature: a small increase in temperature results in a MUCH higher fusion rate. Because fusion is so temperature-sensitive, in a main-sequence star, fusion of hydrogen into helium occurs only in the hot, dense central core.

All main sequence stars (including the Sun) are in hydrostatic equilibrium. That is, the inward force of gravity, which tends to compress the star, is balanced by the outward force due to the pressure. (For a review of hydrostatic equilibrium within the Sun, you can go to the lectures for Wednesday, January 8.)

The observable properties of main sequence stars, such as their surface temperature, luminosity, and radius, are all dictated by the mass of the star. Thus, the main sequence is a MASS sequence.

Consider taking a star and increasing its mass by pouring a little extra hydrogen gas onto it.

Higher mass leads to
Higher compression, which leads to
Higher central density and temperature, which leads to
MUCH faster fusion, which leads to
MUCH higher luminosity.

Because of the extremely sensitive dependence of the fusion rate on temperature, a small change in mass leads to a small change in the central temperature, but a very large change in the luminosity. Expressed mathematically,
L = M^3.5
where L is the luminosity of a main sequence star (in units of the Sun's luminosity) and M is the mass of a main sequence star (in units of the Sun's mass). For instance, a star with a mass of M = 2 M_sun will have a luminosity of
L = 2^3.5 = 11 L_sun

(2) Fusion is stabilized by a natural pressure-temperature thermostat.

Also humans cannot manufacture stars, they have figured out how to make bombs powered by nuclear fusion. In a fusion bomb, the fusion reactions last for only a tiny fraction of a second. In the Sun, fusion reactions have been going on for 4.6 billion years. This leads to the question:
Why doesn't the Sun explode like a hydrogen bomb?
The main reason why the Sun doesn't blow itself to bits in a runaway fusion reaction is that the physical relation among the pressure, temperature, and fusion rate creates a natural thermostat which keeps the center of the Sun (and the center of any other main sequence star) at a steady temperature.

A thermostat is any feedback device which acts to keep the temperature of a system nearly constant. (If you've ever been curious how the thermostat in a home heating system works, you can go to the ``How Stuff Works'' web site.) Basically, when the temperature drops too low, the thermostat increases the rate at which heat is generated. When the temperature rises too high, the thermostat decreases the rate at which heat is generated.

How does a star's natural thermostat work? Consider what would happen if you increased the fusion rate in a star's core:

(1) Core temperature increases
(2) Core pressure increases
(3) Core expands
(4) Core density & temperature decrease
(5) Fusion rate decreases

Thus, increasing the fusion rate sets a chain of events into action whose end result is to decrease the fusion rate again.

Now consider what would happen if you decreased the fusion rate in a star's core:

(1) Core temperature decreases
(2) Core pressure decreases
(3) Core contracts
(4) Core density & temperature increase
(5) Fusion rate increases

(3) High-mass main sequence stars have shorter lifetimes than low-mass stars.

A star's ``lifetime'' on the main sequence is how long it takes to use up the hydrogen in its core. The luminosity (L) of a star is a measure of rapidly it is using up its hydrogen. The mass (M) of a star is a measure of how much fuel it has. The time it takes to use up the fuel is proportional to its amount of fuel (M) divided by the rate of fuel consumption (L). Expressed more mathematically,
t = M/L ,
where t = lifetime (in units of the Sun's lifetime)
M = mass (in units of the Sun's mass)
L = luminosity (in units of the Sun's luminosity.

Note that since L = M^3.5,
t = M/L = M/M^3.5 = 1/M^2.5.

The Sun will not be able to convert all its mass into helium. For one thing, the Sun was not made of pure hydrogen when it formed 4.6 billion years ago. For another, only the hydrogen in the Sun's core is able to be fused; the hydrogen in the Sun's outer layers is at too cool a temperature to fuse. Mathematical models of the Sun's interior lead to the conclusion that the Sun will run out of hydrogen in its core after a lifetime of t_sun = 10 billion years. (Thus, the Sun is middle-aged, nearly halfway through its main sequence lifetime.)

Consider a star of mass M = 0.2 M_sun. Its lifetime will be
t = 1 / (0.2)^2.5 t_sun = 56 t_sun = 560 billion years.

Similar calculations can be done for stars of other masses. Very hot and luminous stars (of spectral type `O' and `B') have short lifetimes; if you see an `O' or `B' main sequence star, you know it must be much younger than the Sun. However, cool and dim stars (of spectral type `K' or `M') have long lifetimes; if you see a `K' or `M' main sequence star, it might be older than the Sun. (On the other hand, it might be younger.)

Prof. Barbara Ryden (ryden@astronomy.ohio-state.edu)

Updated: 2003 Jan 27