Astronomy 162: Professor Barbara Ryden
When the radii and masses of white dwarfs such as Sirius B were first computed, astronomers were flabbergasted. Stars with masses comparable to that of the Sun were scrunched down into a volume comparable to that of the Earth. What is the source of the pressure which keeps white dwarfs from collapsing under their own strong gravitational force?
A white dwarf is supported by a different type of pressure (not dependent on the temperature of the white dwarf): degenerate-electron pressure.
Under the extreme conditions which prevail within a white dwarf, the laws of quantum mechanics become important. Quantum mechanics is the study of how subatomic particles (such as electrons, protons, and neutrons) behave. Subatomic particles do not always obey the same laws as large objects. Hence, the laws of quantum mechanics sometimes seem contrary to common sense.
One rule of quantum mechanics (known as the Pauli exclusion principle)
is this:
Two identical electrons, located in the same region of space,
cannot have the same velocity.
In a dense white dwarf, where the electrons are packed
close to each other, some of the electrons are forced
to have high velocities, and hence provide a high pressure.
In a degenerate object such as a white dwarf, the fast-moving
high-energy electrons provide a pressure which is
independent of temperature. Even as the temperature
of a white dwarf falls toward absolute zero, the
Pauli
exclusion principle demands that the high-velocity electrons
keep moving at the same speed. Hence, the pressure exerted
by the electrons remains
constant as the temperature falls.
The ejected outer layers, heated by the hot new white dwarf, form an emission nebula. An emission nebula of this sort - ejected gas which is being excited by a hot white dwarf - is called a planetary nebula. (This confusing name goes back to the 18th century; viewed through a small telescope, the fuzzy disk of a planetary nebula looks a bit like the fuzzy disk of a planet like Uranus. Viewed with the Space Telescope, however, planetary nebulae like the ``Spirograph Nebula'' and the ``Eskimo Nebula'' show a wealth of fine detail.)
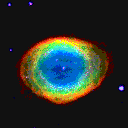
The above picture is of the Ring Nebula, a
planetary nebula in the constellation Lyra. (Click on the
image for a higher-resolution version.) The blue light
in the center of the nebula is emitted by ionized helium.
In the cooler outer regions of the nebula, the dominant
sources of emission are hydrogen and oxygen.
The central hot white dwarf is visible as a point of
light in the center of the nebula.
(Image credit: N. Lame and R. Pogge [OSU])
Measuring the Doppler shifts of planetary nebulae reveals that they are expanding. A typical middle-aged planetary nebula will be about a light year across. A planetary nebula will last for about 50,000 years before fading into invisibility.
After the planetary nebula fades, the white dwarf will still be visible. White dwarfs shine because they are hot; although a white dwarf has no internal power source, it takes billions of years for a white dwarf to cool down. Thermal energy in the interior of a white dwarf is carried to the surface by conduction, then radiated away.
As the temperature T of the white dwarf's surface decreases, the radius R remains constant. (Remember the degenerate-electron pressure which supports a white dwarf is not dependent on T; thus, hydrostatic equilibrium is maintained even as the white dwarf cools.) Since T decreases and R is constant, the luminosity L decreases. The oldest, coldest white dwarfs have L = 0.0001 Lsun and T = 5000 Kelvin. In the future, the eventual fate of a white dwarf will be to become a black dwarf (not to be confused with a black hole). A black dwarf is an extremely cold compact object supported by degenerate-electron pressure.
You can't have a white dwarf more massive than 1.4 Msun.
Asymptotic giant branch stars lose matter into space at a rapid rate. It is possible for fairly massive stars to slim down to below the Chandrasekhar limit by the time they collapse into white dwarfs. A star with a main sequence mass of 4 Msun, for instance, will lose about 2.6 Msun into outer space, and will end as a 1.4 Msun white dwarf. Stars which are more massive than about 4 Msun during their main sequence lives will NOT be able to lose enough mass to become white dwarfs.
Updated: 2003 Jan 30
Copyright © 2003, Barbara Ryden