
The shortest distance between two points is a straight line.
Parallel lines never meet.
Astronomy 162: Professor Barbara Ryden
Newton's view:
Mass tells gravity how to exert a force ( F = G M1 M2
/ d2 );
Force tells mass how to accelerate (F = M2 a).
Einstein's view:
Mass-energy tells spacetime how to curve;
Curvature tells mass-energy how to move.
What do we mean when we talk about the curvature of spacetime? Spacetime has four dimensions (3 space dimensions, 1 time dimension); the curvature of a four-dimensional volume is very difficult to visualize, to put it mildly!
For the purposes of visualization, consider a two-dimensional surface.
On a flat surface, like a tabletop:

The shortest distance between two points is a straight line.
Parallel lines never meet.
On a curved surface, like a globe:
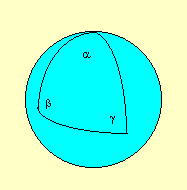
The shortest distance between two points is a curved
line (on a spherical globe, the shortest distance is a great circle).
Parallel lines converge or diverge (on a spherical globe, parallel
lines converge).
Just as you can have flat or curved two-dimensional surfaces, you can have flat or curved four-dimensional volumes.
Einstein would say, ``A massive object curves the spacetime around it. Freely falling objects will follow the shortest path between two points, and hence will follow curved lines in the curved spacetime.'' Einstein would also point out that photons follow curved paths in spacetime as well, even though they have no mass.
As an analogy to Einstein's view of gravity, consider a rubber sheet which is held taut on a frame. It is flat, so if you roll a marble across it, the marble will follow a straight line. Now drop a heavy ball bearing onto the rubber sheet. The ball bearing is massive enough to cause a depression in the rubber sheet around it. Now roll a marble across the rubber sheet, close to the ball bearing. The curvature of the rubber sheet will cause the marble to follow a curved path. A distant observer, unable to see the curvature in the rubber sheet, would say ``The ball bearing must be exerting a force on the marble, deflecting it from its straight path.''
Thus, an object which is following the shortest path on a curved surface looks as if a force is being exerted on it. Similarly, an object following the shortest path in a curved four-dimensional spacetime will look as if a force (the force of gravity) is being exerted on it.
There have been three major experimental tests of the theory of General Relativity, ALL of which support Einstein over Newton.
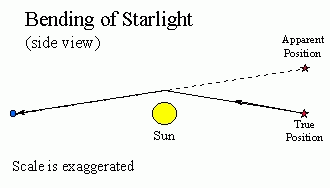
The actual prediction of Einstein is that starlight passing close to the Sun will be deflected by only 1.75 arcseconds (a small but measurable amount). During a total solar eclipse in 1919, astronomers tested Einstein's prediction by photographing the apparent position of stars close to the Sun and comparing them to the true position, measured 6 months earlier when the Sun was on the opposite side of the celestial sphere. The results are shown below. The small blue circles represent the true positions of stars; the arrows point to their apparent positions when the Sun was in their midst.
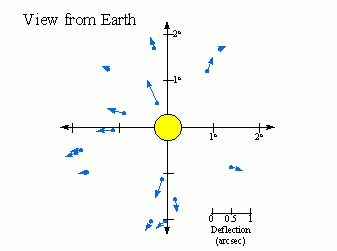
The observations agree (within experimental error) with Einstein's prediction.
Score: Einstein 1, Newton 0.

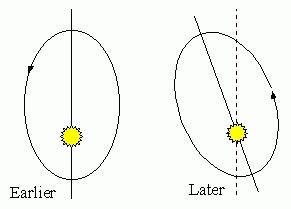
Part of the precession is explained by the perturbing force of the gravity of the other planets. However, the amount of the precession is 43 arcseconds/century greater than is predicted by Newton's theory. This doesn't sound like a large effect; it will take over 3 million years to twist the orbit of Mercury through 360 degrees. However, it was large enough to throw astronomers into a tizzy at the end of the 19th century. (They actually hypothesized the presence of an additional planet, called Vulcan, with an orbit smaller than that of Mercury. )
The additional precession of 43 arcsec/century, however, is precisely equal to the precession predicted by Einstein's theory (when Mercury is at perihelion, the greater spacetime curvature gives the orbit of Mercury a little extra twist). The hunt for the planet Vulcan could be called off.
Score: Einstein 2, Newton 0.
Score: Einstein 3, Newton 0.
Not so fast...Newton's theory gives highly accurate results when speeds are slow and gravity is weak (this is true almost everywhere). Moreover, computing Newtonian forces is simpler than computing the full four-dimensional relativistic curvature, so astronomers, who like a simple life, use the theory of Newton whenever possible, resorting to the accuracy of Einstein's Theory of General Relativity only when absolutely necessary.
Updated: 2003 Feb 11
Copyright © 2003, Barbara Ryden