Astronomy 162: Professor Barbara Ryden

Wednesday, February 12

BLACK HOLES

``The gates of hell are open night and day;
Smooth the descent, and easy is the way:
But to return, and view the cheerful skies,
In this the task and mighty labor lies.''
- Virgil, The Aeneid, Book VI
[John Dryden translation]

Key Concepts

A collapsing stellar core with M > 3 M_sun will become a black hole.
If anything enters the event horizon of a black hole, it cannot escape again.
Near a black hole, spacetime is severely distorted.

(1) A collapsing stellar core with M > 3 M_sun will become a black hole.

If the initial mass of a star is greater than 20 M_sun or so, its supernova explosion leaves behind a dense core with M > 3 M_sun. Since it is too massive to become a neutron star, the dense core collapses totally. Nothing can stop its infall; according to the laws of physics, taken to their logical conclusion, it becomes a singularity. A singularity is a point which has zero radius and infinite density.

An object with infinite density is distressing to think about (it was bad enough contemplating a neutron star with a density of 400 million tons per cubic centimeter!) Fortunately for the sanity of astronomers, it is impossible to see a singularity, because its escape speed is too high.

The escape speed V at a distance R from a mass M is given by the formula:
V = ( 2 G M / R )^1/2 ,
where G is Newton's gravitational constant. For instance, at the surface of the Sun (whose mass is 2 x 10³⁰ kilograms), you are at a distance R = 700,000 kilometers from the Sun's center. The escape speed from the Sun's surface can be computed to be V = 620 kilometers/second. At R = 1 AU = 150,000,000 kilometers from the Sun's center, the escape speed from the Sun is only V = 42 kilometers/second. The farther you get from a massive object, the lower the escape speed is.

At a very great distance from a singularity of mass M, the escape speed is tiny. As you approach the singularity, however, and R steadily decreases, the escape speed V becomes higher and higher. At a critical radius, known as the Schwarzschild radius, the escape speed becomes equal to the speed of light.

The numerical value of the Schwarzschild radius, R_s, is given by the equation:

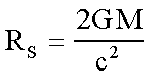
where G is Newton's gravitational constant, and c is the speed of light. In practical units,
R_s = 3 kilometers ( M / 1 M_sun )
In other words, a singularity with a mass equal to that of the Sun will have a Schwarzschild radius of only 3 kilometers. The Schwarzschild radius is directly proportional to the mass of a singularity.

A black hole is defined as ANY object which is smaller than its Schwarzschild radius. For instance, take an astronomy professor with a mass of M = 70 kilograms. Squeeze her down to a sphere with radius R = 10^-25 meters, and she will be a black hole.

In theory, a black hole can have any mass; take an object of any size and squeeze it down to its Schwarzschild radius - instant black hole. The collapse of massive stars is merely a convenient means of making black holes with masses of M = 3-10 M_sun and Schwarzschild radii of R_s = 9-30 kilometers.

(2) If anything enters the event horizon of a black hole, it cannot escape again.

Draw a sphere of radius R_s around a singularity. This sphere is known as the event horizon. Inside the event horizon, the escape speed from a singularity is greater than the speed of light. Since nothing can travel faster than the speed of light, nothing can escape from inside the event horizon.

A black hole can be thought of as a Cosmic Lobster Trap; objects can enter the event horizon easily enough, but nothing (not even light) can come out. Here in the outside universe, we have no information whatsoever about what is going on inside an event horizon. We presume that once a dense stellar core is compressed into a black hole, it goes on to become a singularity; that is what the laws of physics predict. However, we have no way of confirming this prediction by observation from outside the event horizon. If you entered the event horizon, you would be able to discover whether there's a singularity inside. However, you wouldn't be able to communicate your results to anyone outside the event horizon. Information cannot travel from inside an event horizon to outside an event horizon.

In cheap science fiction stories, black holes are sometimes described as if they are ``cosmic vacuum cleaners'', sucking up everything in their path with the malevolent force of their gravity. Black holes are much more benign than that. Black holes are inescapable only if you venture inside the event horizon. The event horizon of a black hole which forms from a collapsing star is quite small - only 10 miles or so in radius.

(3) Near a black hole, spacetime is severely distorted.

Close to the event horizon of a black hole, space and time are strongly warped, according to the tenets of General Relativity. As seen by an observer far outside the event horizon:

Clocks closer to the event horizon run more slowly.
Photons originating near the event horizon are strongly redshifted.
Photons passing near the event horizon are strongly deflected.

To illustrate some of the effects of spacetime distortion, let's take an imaginary Journey into a Black Hole.

Suppose you are orbiting a black hole at a safe distance (well outside the event horizon). Unwilling to make the one-way trip inside the event horizon yourself, you drop a warthog - snout first - toward the black hole, after tying a flashing blue light to the warthog's tail. As the warthog drops toward the event horizon, what happens? Well, as frequently happens in life, what you see depends on where you are.

What you see (the outside view)

As the warthog approaches the event horizon, you see:

The beacon flashes more slowly.
The beacon becomes redder (even shifting to radio wavelengths).
The beacon becomes dimmer.

Eventually, in the far distant future, your descendants will see a faint, ghostly image of the warthog, moving excruciatingly slowly, never quite reaching the event horizon.

What the warthog sees (the inside view)

As the warthog approaches the event horizon, it sees:

The beacon flashes at a constant rate.
The beacon's color is the same.
The beacon is of constant brightness.

In short, the warthog sees nothing unusual in its immediate vicinity. It passes through the event horizon with nothing unusual happening to mark the boundary crossing.

Unfortunately, as the warthog approaches the singularity, it will be ripped apart by incredibly strong tidal forces. The gravitational pull on its snout will be much stronger than the pull on its rump, and it will be shredded. (The ASPCA would definitely not approve of this experiment...)

Still curious? Try this page of Frequently Asked Questions about black holes.

For cheap visual thrills, try a Virtual Trip to a Black Hole, demonstrating some of the bizarre relativistic effects that take place close to black holes.

Prof. Barbara Ryden (ryden@astronomy.ohio-state.edu)

Updated: 2003 Feb 12