First assumption of cosmology: the universe is homogeneous on large scales. ``Homogeneous'' merely means that every region of the universe is pretty much the same as every other region; there are no special locations. On small scales, the universe is obviously very inhomogeneous; it's full of lumps. Stars are much denser than the interstellar medium. Galaxies are much denser than the intergalactic medium. Even superclusters are denser than the voids between them. HOWEVER, on scales larger than superclusters and voids (> 100 Mpc), the universe is finally homogeneous. The average density of stuff within a sphere of radius 100 Mpc is the same as the average density of any other sphere of the same size.
Second assumption of cosmology: the universe is isotropic on large scales. ``Isotropic'' merely means that every direction in the universe is pretty much the same as every other direction; no matter which way you look, you see the same view. On small scales, the universe is obviously anisotropic; there exist preferred directions. Look down & you see rock; look up & you see sky. Look toward the Virgo cluster & you see lots of galaxies; look away from the the Virgo cluster & you see fewer galaxies. HOWEVER, on scales larger than superclusters and voids (> 100 Mpc), the universe is finally isotropic.
Another assumption of cosmology (and of all fields of science) is that the laws of physics are universal; that is, they are the same everywhere in the universe. For instance, we assume that Kepler's Third Law applies to a binary galaxies millions of light years away just as well as it applies to planets within the Solar System.
Consider the analogy of an ant wandering
over the surface of an orange. The ant will encounter small
local dimples (the pores of the orange), but if the ant
wanders far enough, it will discover that the orange is
spherical on average.
On large scales, there are three
possibilities for the average curvature of space.

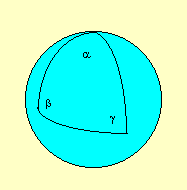

It's hard to tell, since we see only a limited volume within our cosmic particle horizon. It's comparable to the difficulty that early cultures had in determining that the Earth was spherical -- positively curved -- rather than flat. Actually, it's even worse than you might think, since the local curvature due to stars, galaxies, clusters, and superclusters tends to mask the global positive or negative curvature. (Imagine trying to determine the curvature of the Earth if you were confined to Switzerland. The local curvature, due to the Alps, would totally swamp the global curvature due to the Earth's spherical shape.)
The most promising technique for determining the curvature of the Earth involves looking at the angular size of very distant objects, such as ``hot spots'' in the Cosmic Microwave Background. In flat space, light from the hot spots travels along straight lines. In positively curved space, though, light travels along converging lines. This has the effect of making the hot spots look larger than they would in flat space. Conversely, in a negatively curved space, the hot spots would look smaller than they would in flat space. As it turns out, the actual size of hot spots (about one degree across) is just what cosmologists would have expected in a flat universe. Precise measurements lead cosmologists to conclude that the universe is flat, and thus has infinite volume. (We can't rule out, however, the possibility that the universe has a tiny amount of positive curvature, leading to a universe whose volume is finite, although very very much larger than the volume within our cosmic particle horizon.)
The mass of clusters of galaxies can be determined by the application of Kepler's Third Law to galaxies within the cluster. A census of all the clusters of galaxies within a few hundred Mpc of us leads to the conclusion that the mass in clusters only amounts to 30 percent or so of the critical density. What provides the rest of the mass (or energy) required to flatten the universe? The Cosmic Microwave Background, although it has no mass, has energy. Every cubic meter of space contains about 400 million CMB photons. The total energy of all those photons contributes 4 x 10-14 joules per cubic meter. If you divide this energy density by c2 to find an equivalent mass density, it comes to merely 5 x 10-31 kilograms per cubic meter, only 0.005 percent of the critical density. The Cosmic Microwave Background doesn't contribute significantly toward flattening the universe. (And starlight doesn't help, either; all the light emitted by stars during the past 14 billion years has an average energy density less than the Cosmic Microwave Background.)
Where is the rest of the mass (or energy) hidden? [Come back next week for a further discussion of the mysterious hidden energy (or mass)...]
Updated: 2003 Mar 6
Copyright © 2003, Barbara Ryden