Astronomy 171
Solar System Astronomy
Prof. Paul Martini

Lecture 17: Gravity

Key Ideas:

Law of Falling Bodies (Galileo): All falling bodies experience the same gravitational acceleration
Law of Universal Gravitation (Newton): Gravity is an attractive force between all pairs of massive objects; Gravitational force is proportional to the masses, and inversely proportional to the square of the distance between them.

The Law of Falling Bodies

Prior to his telescopic work, Galileo performed fundamental research on motion.
Explored the rate of falling bodies by dropping different weights, or sliding them down inclined planes.
Law of Falling Bodies:: In the absence of air, heavy objects and light objects fall at the same, constant rate of acceleration.

Apollo 15 Hammer-Feather Drop

Commander David Scott dropped a hammer and a feather on the surface of the Moon to illustrate that Galileo's Law of Falling Bodies was correct. The movie shown in class is available from NASA's Apollo 15 Hammer-Feather Drop webpage.

Universal Mutual Gravitation

Isaac Newton, in his Principia, formulated the Law of Universal Mutual Gravitation:
Gravity is an Attractive force:: Works to bring massive objects closer together.
Gravity is a Universal force:: Works everywhere in the Universe.
Gravity is a Mutual force:: Works between pairs of massive objects.

Gravitational Force

The Force of Gravity between any two objects depends only upon:
The masses of the two objects:: More massive objects exert a stronger the gravitational force.
The distance between them:: The force gets stronger as the two objects move closer together.; The force gets weaker as the two objects move farther apart.
It does not depend on the shapes, colors, or compositions of the objects.

The Law of Universal Gravitation

The force of gravitational attraction between any two massive bodies is proportional to their masses and inversely proportional to the square of the distance between their centers.

The Force of Gravity is an example of an "Inverse Square Law Force"
Stated Mathematically:
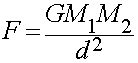
Where:: F = force due to gravity.; M₁ = mass of the first object; M₂ = mass of the second object; d = distance between their centers.; G = "Gravitational Force Constant"

The Gravitational Force Constant

The force constant, G, is a number which gives the size of the gravitational coupling between two massive objects.
G is very small, in metric units: G=6.7x10^-11 Newtons meter² / kilogram²
The Newton is the metric unit of force:

4.41 Newtons = 1 pound
G has to be measured experimentally.

The Fall of an Apple.

Stand on the Earth and drop an apple.
What is the force of the Earth on the apple? F = GM_E M_apple/R_E²
What is the apple's acceleration (2nd Law): a_apple = F/M_apple = GM_E/R_E² = 9.8 meters/sec²
Note that the mass of the apple (M_apple) had divided out of the equation. This means that the acceleration due to gravity is independent of the mass of the apple, just like Galileo had shown earlier.

Equal and Opposite Reactions

But, the third law says that all forces come in equal yet opposite pairs.
What force does the the apple apply in return upon the Earth? F = GM_E M_A/R_E²
How much does the Earth accelerate towards the apple? a = F/M_E = GM_A/R_E² = 9.8 m/sec² x (M_A/M_E) = very small amount (about 10^-25 meters/sec²)

The Mass of the Earth

We can directly measure the acceleration of gravity at the surface of the Earth by dropping objects and timing their fall (e.g., like was done by Galileo). We find a = 9.8 meters/sec²
We can also measure the radius of the Earth using geometry (Eratosthenes): R_E=6378 kilometers = 6,378,000 meters
Combining these together using Newton's formula for the Gravitational Force allows us to estimate the mass of the Earth, as follows:
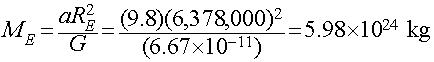
This is an example of one of the powerful implications of Newton's Law of Gravity: It gives us a way to use the motions of objects under the influence of their mutual gravitation to measure the masses of planets, stars, galaxies, etc.

The Orbit of the Moon

Falling apples are one thing, but what about the Moon?: What keeps the Moon in orbit around the Earth?
The Law of Inertia (Newton's 1st law) predicts: If there were no gravitational force acting between the Moon and the Earth, the Moon would travel in a straight line at a constant speed.
But, of course the Moon really moves along a curved path:: It is deflected from a straight-line path by the force of gravity.
This causes the Moon to fall a little bit towards the Earth at the same time at it moves to one side.

The Fall of the Moon

How far does the Moon "fall" around the Earth in 1 second?; Newton computed this. In order to stay in its orbit, the Moon must fall by 0.00136 meters (about 1.4 mm) each second.; Call this quantity x_moon, the deflection of the orbiting moon in 1 second.
How far does an apple fall on the Earth during the first second?: Newton also knew this (he could measure it directly), it falls 4.9 meters in the first 1 second.
Call this quantity x_apple, the deflection of a falling apple in its 1 second of motion.

Newton also knew that:

Moon is about 60 Earth Radii from the Earth.

Summarizing the numbers:

The Moon:

Distance that the Moon falls towards Earth in 1 second: x_moon = 0.00136 meters

The distance of the Moon from the center of the Earth: d_moon = 60 R_E

Acceleration of the Moon: a_moon = GM_E/d_moon² = GM_E / (60R_E)²

The Apple:

Distance the an Apple falls on Earth in 1 second: x_apple = 4.9 meters

The distance of the Apple from the center of the Earth: d_apple = 1 R_E

Acceleration of the Apple: a_apple = GM_E/d_apple² = GM_E/R_E²

The ratio of the deflections of the Apple and the Moon in 1 second will be proportional to the ratio of how much they have been accelerated during that 1 second.

Putting all the info we have together, we get the following:

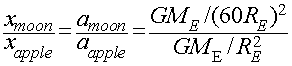
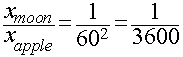
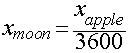
This predicts that the deflection of the moon in 1 second necessary to keep it in orbit around the Earth should be 1/3600^th the deflection of an apple during the first second of its fall to the Earth.

Is this right?

Recalling that from before, we found that the deflections of the moon and apple in 1 second are:

x_moon = 0.00136 meters

x_apple = 4.9 meters

Gravity predicts that

x_apple/3600 = 4.9 meters/3600 = 0.00136 meters!!

The agreement is essentially perfect!

This demonstrates that the same law of gravity applies to both the apple and the Moon! Both feel the gravity of the Earth in the form of a force that gets weakers as the square of their distance from the center of the Earth.

So why does the Moon orbit the Earth?

If the Moon is falling a little towards the Earth, just like an apple dropped on the surface, why does the Moon travel around the Earth in an orbit instead of falling onto it?
The way to answer this question is to first consider what would happen if there was no gravity acting:

Question: How far would the Moon travel in a straigth line in 1 second if there were no gravity acting?
Answer: About 1000 meters.

At the same time, the Moon's motion along this straight-line path would also cause it to move away from the Earth.

Question: How far away from the Earth would the Moon move in 1 second if no gravity were acting?
Answer: About 0.00136 meters!

In round numbers, the amount the Moon falls towards the Earth due to gravity is just enough to offset the straight-line path it would take if gravity were not acting to deflect it. This balance effectively closes the loop.

We have therefore reached a startling conclusion:

The Moon is really perpetually falling around the Earth!

This is a totally different way of looking at an "orbit" under the influence of gravity.

While at first sight the fall of an apple and the orbit of the Moon appear to be two completely different phenomena, viewed in light of Newton's laws of motion, they are in fact different manifestations of the same thing! The fall of the Moon around the Earth is the same kind of motion as the fall of an apple to the Earth. Both are described by the same three laws of motion, and both feel a gravitational force described by the same, universal force law.

Universal Gravitation

The Law of Gravity is Universal:: Governs the fall of an apple on the Earth.; Governs the fall of the Moon around the Earth.; Governs the fall of the Earth/Moon system around the Sun.; Governs the fall of the Sun around the center of the Milky Way Galaxy.; Governs the fall of the Milky Way and Andromeda Galaxies in their mutual orbit...
and so on throughout the Universe.

See A Note about Graphics to learn why some of the graphics shown in the lectures are not reproduced with these notes.

[ Return to the Astronomy 171 Main Page | Unit 4 Page ]