Astronomy 171
Solar System Astronomy
Prof. Paul Martini

Lecture 18: Orbits

Key Ideas:

Newton generalized Kepler's laws to apply to any two bodies orbiting each other: First Law: Orbits are conic sections with the center-of-mass of the two bodies at the focus; Second Law: Angular Momentum Conservations; Third Law: Depends on the masses of the bodies
Triumphs of Newtonian Gravity: Predicted return of Halley's Comet; Discovery of Neptune

Kepler's Laws Revisited

First Law:: Orbits are ellipses with the Sun at one focus
Second Law:: Line from Sun to Planet sweeps out equal areas in equal times
Third Law:: P² = a³ where P is in years and a is in AUs.

Newton's Generalization

Newton showed that Kepler's Laws can be derived from first principles:: Three Laws of Motion; Law of Universal Gravitation
Newton generalized the laws to apply to any two bodies moving under the influence of their mutual gravitation: Moon orbiting the Earth; Two stars orbiting each other; And much, much, more

First Law of Orbital Motion

The shape of an orbit is a conic section with the center-of-mass at one focus

Conic Sections:
Curves found by cutting a cone with a plane: Circles, Ellipses, Parabolas, and Hyperbolas
Center-of-Mass is at the Focus: The Earth does not orbit the Sun, the two orbit each other about their mutual center-of-mass.

Closed and Open Orbits

Conic curves come in two families
Closed curves:: Ellipses; Circles: special case of an ellipse with e=0; Orbits are bound and objects orbit perpetually
Open curves:: Hyperbolas; Parabolas: special case of a hyperbola; Orbits are unbound and objects escape

Circular Velocity

Velocity needed to sustain a circular orbit of a given radius, r, from a massive body, M:

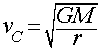
If v<v_C, the orbit is an ellipse smaller than the circular orbit.

Go a little faster than v_C, the orbit is an ellipse larger than the circular orbit,

Go a lot faster, and…

Escape Velocity

This is the minimum velocity required to have a parabolic orbit starting at a given distance, r, from a massive body, M:

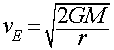
At the Earth's surface:: v_C = 7.9 km/sec (28,400 km/hr); v_E = 11.2 km/sec (40,300 km/hr)

Center of Mass

Two objects orbit about their center of mass: Balance point between the two masses; Semi-Major axis is a = a1 + a2; Relative positions a2/a1 = M1/M2

Example: Earth and Sun

M_sun = 2 x 10³⁰ kg

M_earth = 6 x 10²⁴ kg

From the balance relation, the distances of the sun and earth from their mutual center of mass are related to the size of the semi-major axis of the Earth's orbit (a) and the ratio of the masses:

a_sun + a_earth = 1 AU = 1.5 x 10⁸ km

a_sun/a_earth = M_earth/M_sun = 3 x 10^-6

After some simple algebra, we find:

a_sun = 450 km

Since the radius of the Sun is 700,000 km, this means that the center-of-mass of the Earth-Sun system is deep inside the Sun.

Second Law of Orbital Motion

Orbital motions conserve angular momentum
Angular Momentum:: L = mvr = constant
where:: m = mass; v = velocity; r = distance from the center of mass
At constant mass:: Increase r, v must decrease proportionally; Decrease r, v must increase proportionally

Angular Momentum and Equal Areas

Motion of a planet around the Sun conserves angular momentum
Near Perihelion:: Planet is closer to the Sun (smaller r); Speed (v) increases to compensate
Near Aphelion:: Planet is farther from the Sun (larger r); Speed (v) decreases to compensate

Third Law of Orbital Motion

Newton's generalization of Kepler's 3rd Law:

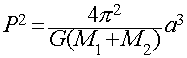
Where:: P = period of the orbit; a = semi-major axis of the orbit; M₁ = mass of the first body; M₂ = mass of the second body

A Third Law for Every Body

The proportionality between the square of the period and the cube of the semi-major axis now depends on the masses of the two bodies.

For planets orbiting the Sun, M_sun is so much bigger than any planet (even Jupiter, at 1/1000^th M_sun), that we recover Kepler's version of the Third Law from Newton's more general form:

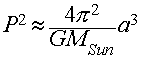
Measuring Masses

Newtons' form of Kepler's 3rd Law lets us measure masses from orbital motions!
Mass of the Sun from the Earth's orbit:: Period = 1 year = 3.156 x 10⁷ seconds; a = 1 AU = 1.496 x 10¹¹ meters

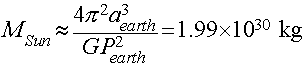
Universal Method for Masses

Measure mass of Jupiter from the orbits of the Galilean moons, since M_Jupiter >> M_moons: Find M_Jupiter ~ 300 M_Earth
Measure the mass of the Earth and Moon by measuring their orbital parameters:: Earth is 81x more massive than the Moon
Can also measure the masses of binary stars

Predictive Power of Gravity

Halley's Comet:: Using Newtonian Gravity, Edmond Halley found that the orbit of the Great Comet of 1682 was similar to comets seen in 1607 and 1537.; He predicted it would return again in 1758; It was seen again Christmas night 1758
Dramatic confirmation of Newton's Laws of Motion and Gravitation

Discrepant Orbit of Uranus

In 1781, William Herschel accidentally discovered the 7th planet: Uranus
By 1840, the discrepancies between the predicted and actual positions of Uranus were larger than 1 arcminute: Likely cause was the gravitational tug of an 8th, as yet unknown, massive planet beyond Uranus; Adams in the UK and Leverrier in France began calculations based on Newtonian Gravity

The Discovery of Neptune

Using the discrepant motinos of Uranus, they predicted where the unknown 8th planet should be
On Sept 23, 1845, Galle found Neptune only 52 arcminutes from its predicted location!
This was a great triumph for Newtonian Gravity.

The Why of Planetary Motions

Kepler's Laws are descriptions of the motion:: Arrived at by trial and error, and some vague notions about celestial harmonies; Only describe the motions, without explaining why they move that way
Newton provides the explanation: Kepler's Laws are a natural consequence of Newton's 3 Laws of Motion and his Law of Gravitation; Gives the laws predictive power

See A Note about Graphics to learn why some of the graphics shown in the lectures are not reproduced with these notes.

[ Return to the Astronomy 171 Main Page | Unit 4 Page ]