Lecture 13: The Harmony of the Spheres:
Greek Astronomy

Key Ideas:

Early Geocentric Systems:

Early Heliocentric System:

Epicyclic Geocentric Systems:

Summary of Celestial Motions

Fixed Stars:

The Sun:

The Moon:

The Planets:

Any successful description of the Solar System must explain all these facts.

The Geocentric System

Geocentric = Earth-Centered

Anaximander of Miletus (611-546 BC)

Among the first Greek philosophers to suggest a geocentric system:

This was an interesting mix of old (flat earth) and new ideas that set the basic themes for much of what was to follow.

Pythagoras of Samos (569-475 BC)

Philosopher & Mathematician, founded the Pythagorean school. Taught that spheres are the perfect geometric shapes.

Pythagorean Model:

Vibrations from their rubbing together created a harmonious "Music of the Spheres.

Eudoxus of Cnidos (b. 408 BC)

A pupil of Plato, Eudoxus elaborated a geocentric model composed of crystalline spheres, incorporating the Platonic ideal of uniform circular motion.

System of 27 Spheres:

Spheres within spheres in perfect circular motion combine to give retrograde motions.

Spheres within Spheres


(Click on the image to view at full scale [Size: 20Kb])

Four Spheres for each planet:

All were in uniform circular motion about their axes.

Aristotle (384-322 BC)

Another pupil of Plato, the tutor of Alexander the Great, and considered the greatest general authority in antiquity. Aristotle wrote about virtual everything known at his time.

His On the Heavens refined Eudoxus' system:

Incorporated physical reasoning:

Earth, Air, Fire, & Water

The Aristotelian World View made certain basic assumptions:

A rotating or revolving Earth would thus be unnatural in this world view.

Preserving Appearances

The models proposed sought primarily to "preserve appearances":

The Aristotelian view of the world was that planetary motions belonged to the perfect celestial realm, and were thus to be understood without needing to inquire as to their physical "causes". In this sense, Aristotle linked Astronomy with Mathematics, where one explored, say, the geometric properties of triangles without any need to ask why they were that way. Mathematics and Astronomy were seen as expressions of perfection in and of themselves. This is unlike the study of Physics, which to Aristotle was concerned with understanding the causes of phenomena in the ever-changing realm of the Earth. This conceptual separation of Astronomy from Physics was to have a profound impact upon the Medieval and Renaissance mind centuries later.

The Heliocentric System:

Heliocentric = Sun-Centered

Alternative viewpoint to Geocentric:

The complex non-uniform and retrograde motions are now just a consequence of viewing moving planets from a moving Earth.

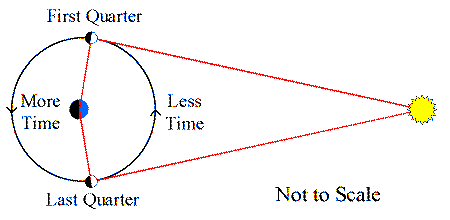
Aristarchus of Samos (310-230BC)

Proposed a Heliocentric system. It seems that his reasoning was the large size he found for the sun.
(Click on the image to view at full scale [Size: 9Kb])

We know none of the details of Aristarchus' Heliocentric model. We only have his treatise on the distances and sizes of the Moon and the Sun, from which we gather what his motivations might have been. We know of his Heliocentric model only from mention of it (usually dismissively) by others who came after him. In particular, Archimedes discussion of it in his Sand Reckoner is our best source.

The heliocentric idea never caught on, perhaps because it was considered too radical given deeply ingrained notions about uniform circular motion and the immobility of the Earth.

Hipparchus of Nicaea (165-127 BC)

Greatest astronomer of the classical period:

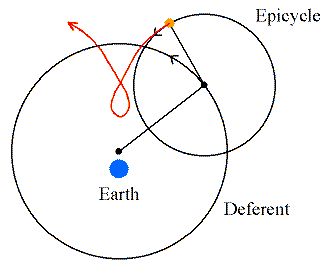
Developed a New and Improved Geocentric System:


(Click on the image to view at full scale [Size: 7Kb])

The main circle is the Deferent, upon which rotates the center of the secondary circle called the Epicycle to which the planet is affixed. The two rotate at different rates, fine-tuned to make the apparent motions as seen from the Earth come out right. Additional epicycles are added to further fine-tune the system. Notice that the Earth is not exactly at the center, but slightly offset at the "eccentric" point.

Successes of Epicycles & Eccentrics

Epicyclic models have a number of successes:

Note:

What distinguishes Hipparchus' geocentric model from all previous models is that it was firmly grounded in observational data, many observations of which he made himself (by all accounts Hipparchus was the supreme observational astronomer of the classical period). In many ways, this work marks a turning point between models motivated primarily by philosophical aesthetics and models based at least in part upon observational data. Hipparchus still sought to preserve appearances, and chose a reasonable (to him) geometric model to represent planetary motions mathematically.

Claudius Ptolemais (Ptolemy - c. 150 AD)

Astronomer and Geographer of the late classical age based at Alexandria, then a colonial outpost of the Roman Empire.

Wrote the Mathematical Syntaxis:

Elaborated Hipparchus' geocentric system, adding extra features to better preserve appearances.

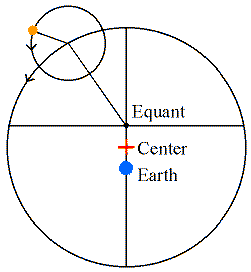
The Equant

Ptolemy introduced the Equant, a geometric "device" to account for observed changes in a planet's speed as it moved around the Earth.


(Click on the image to view at full scale [Size: 6Kb])

This is a very complex construction that, again, was introduced to preserve appearances, this time by replacing the pure Aristotelian and Platonic ideal of Uniform Circular Motion with a slightly modified notion of uniform angular motion about the equant.

The Ultimate Geocentric System

Ptolemy's final geocentric system was quite complex:

It was to prevail virtually unchallenged for nearly 1500 years.

Return to [Unit 3 Index | Astronomy 161 Main Page]
Updated: 2005 October 7
Copyright © Richard W. Pogge, All Rights Reserved.