An Introduction to Solar System Astronomy
Prof. Richard Pogge, MTWThF 9:30
|
|
Astronomy 161: An Introduction to Solar System Astronomy Prof. Richard Pogge, MTWThF 9:30 |
Key Ideas:
Newton generalized Kepler's laws to apply to any two bodies orbiting each other
Kepler's Laws of Planetary Motion are as follows:
Newton showed that Kepler's Laws can be derived from
Further, Newton generalized the laws to apply to any two bodies moving under the influence of their mutual gravitation. For example, these laws apply equally to
The shape of an orbit is a conic section with the center of mass at one focus.There are two parts to Newton's formulation of Kepler's First Law:
Shapes of Orbits are Conic Sections:
The Center of Mass is at the Focus:
These are curves formed by the intersection of a cone and a plane cutting it at various angles.
Conic curves come in two families:
Closed Curves:
Open Curves:
At the Earth's surface:
The picture below illustrates the various types of closed and open
conic-section orbits, all starting from a common point, P, marked on the
right (where all 5 curves intersect).
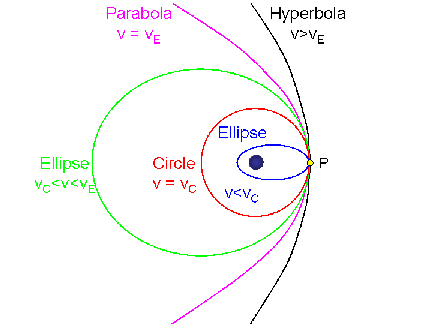
[Click on the image to view a full-size version (9k GIF)]
Thus, which orbit you will be in starting from a given point (labeled P here) is determined by your speed at that point:
Two objects orbit about their center of mass:
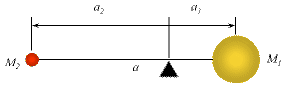
From the balance relation, the distances of the sun and earth from their mutual center of mass are related to the size of the semi-major axis of the Earth's orbit (a) and the ratio of the masses:
After some simple algebra (do it!), we find:
Since the radius of the Sun is 700,000 km, this means that the center-of-mass of the Earth-Sun system is deep inside the Sun.
Orbital motions conserve angular momentum.
This doesn't sound much like "equal areas in equal times", but in fact it is the same thing.
Angular Momentum:
L = mvr = constant
Angular Momentum is "conserved" means L is a constant.
If the distance changes, the velocity must change to compensate so as to keep L constant:
Near Perihelion:
Near Aphelion:
A familiar example of the same principle at work is a figure skater doing a spin. In an "upright spin", the skater stands on one leg with arms outstretched and spins about an up/down axis. The spin is accelerated by the skater drawing in his/her arms. By drawing in his/her arms, they are moving mass closer to the center of their body, and conservation of angular momentum demands that they spin faster.
Newton's Generalization of Kepler's 3rd Law:
The proportionality between the square of the period and the cube of the semi-major axis now depends on the masses of the two bodies.
For planets orbiting the Sun, Msun is so much bigger than any planet (even Jupiter, at 1/1000th Msun), that we recover Kepler's version of the Third Law from Newton's more general form:
Note that the constant of proportionality is the same for all planets (to a good approximation, certainly to within Kepler's data from Tycho).
In Kepler's version, the constant of proportionality works out to be 1.0 if we use units of years for P and AUs for the semi-major axis, a. While computationally convenient, it hides the underlying dependence on the mass of the Sun from sight. The problem with empirical laws, like Kepler's formulation, is that they only show the surface, not the important details underlying them.
Newton's generalized form of Kepler's 3rd law gives us a way to measure masses from orbital motions!
For exampl, we can derive the mass of the Sun by using the period and size of the Earth's orbit:
Using Newton's Form of Kepler's 3rd law for the solar system above, we see that once we know P and a (G and pi are constants), the only unknown is the Mass of the Sun, which can be solved for easily after a little light algebra:
(You can verify the numbers for yourself by using G=6.67 x 10-11 Newton m2/kg2, and the values of P and a for the Earth given above in seconds and meters. Do it!).
The generalized form of Kepler's Third law gives us a powerful tool for measuring the masses of objects by measuring the periods and sizes of their orbits. For example:
We can measure the mass of Jupiter from the orbits of the Galilean moons, since MJupiter>>Mmoons
We can measure the total mass of the Earth and Moon system.
We can measure the masses of binary stars using the full formula and by observing their orbit parameters (you will see this done in Astronomy 162).
Newton's description of planetary positions is only a start.
It also allows quantitative new predictions.
Halley's Comet:
In 1781, William Herschel discovered the planet Uranus orbiting beyond Saturn.
By 1840, the discrepancies between the predicted and actual positions of Uranus grew larger than 1 arcminute.
Two theorists, Urban Leverrier in France and John Couch Adams in the UK, predicted that the deviations were due to the gravitational influence of another, unknown massive planet beyond Uranus.
Using the deviant motions of Uranus, they independently calculated where this unknown 8th planet should be.
On Sept 23, 1845, Galle found Neptune only 52 arcminutes from where Leverrier predicted it would be!
Kepler's Laws are descriptions of the motion:
Newton provides the explanation:
By adding the "why", Newton gave his laws predictive power, and allows us to use them as tools to explore the Universe, both figuratively and literally. We can predict new phenomena or understand oddities in the motions (they laws give us a framework in which to interpret data), and we can literally use them to fly spacecraft through the solar system.