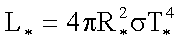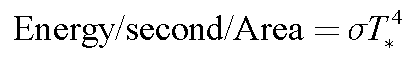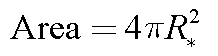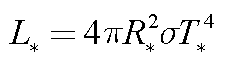|
Astronomy 162:
Introduction to Stars, Galaxies, & the Universe
Prof. Richard Pogge, MTWThF 9:30
|
Lecture 10: Synthesis:
The Hertzsprung-Russell Diagram
Readings: Chapter 19, section 19-7 & 19-8
- Luminosity-Radius-Temperature Relation for stars.
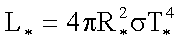
- The Hertzsprung-Russell (H-R) Diagram of stars
- A plot of Stellar Luminosity vs. Effective Temperature
- H-R Diagram Features:
- Main Sequence (most stars)
- Giant & Supergiant Branches
- White Dwarfs
- Luminosity Classes
Summary of Stellar Properties
Large range of Stellar Luminosities:
Large range of Stellar Radii:
Modest range of Stellar Temperatures:
Wide Range of Stellar Masses:
The Luminosity of a star (the total energy emitted per second)
depends on two quantities:
- The "Effective Temperature" of the stellar photosphere, T*
- The total surface area of the star, which depends on its radius, R*
Because stars are hot dense balls of gas, they obey the Stefan-Boltzmann Law
that relates the amount of energy emitted per second from each square
meter of its surface to the temperature of the star:
Stefan-Boltzmann Law:
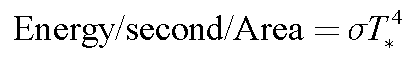
The total surface area of a spherical star is:
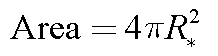
Combining these two, the total Stellar Luminosity
(energy emitted per second) is therefore:
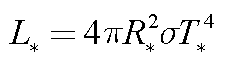
This is the Luminosity-Radius-Temperature Relation for stars.
- In words:
- "The Luminosity of a star is proportional to
its Effective Temperature to the 4th power and its Radius
squared."
- Example 1:
- Two stars are the same size, (RA=RB), but star
A is 2x hotter than star B (TA=2TB):
- Therefore: Star A is 24 or 16x brighter than Star B.
- In words: "If two stars are the same size, the hotter
star is brighter."
- Example 2:
- Two stars have the same effective temperature,
(TA=TB), but star A is 2x bigger than star B
(RA=2RB):
- Therefore, Star A is 22 or 4x brighter than Star B.
- In words: "If two stars have the same effective
temperature, the larger star is brighter."
Hertzsprung-Russell Diagram
Plot of Luminosity versus Effective Temperature for stars:
- estimate the effective temperature, T, from its Spectral Type
- estimate the luminosity, L, from its Apparent Brightness & distance
Plot Temperature from hottest to coolest along the horizontal axis, and
Luminosity from faintest to brightest along the vertical axis:
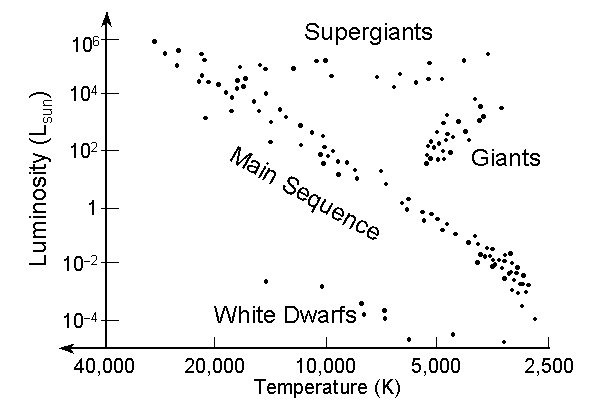
This diagram was first made independently in 1911 by Danish astronomer
Ejnar
Hertzsprung (1873-1967) who plotted the diagram for nearby clusters
of stars (the Hyades and Pleiades), and American astronomer Henry
Norris Russell (1877-1957) who plotted the diagram for nearby stars
in 1913. The form of the diagram we use today is Russell's.
As you can see, stars don't land just anywhere on the H-R Diagram, but
fall in one of a number of specific regions, as follows:
Main Sequence
Most nearby stars (85%), including the Sun, lie along a diagonal
the band in the H-R Diagram called the Main Sequence
- Ranges of stellar properties:
- L=10-2 to 106 Lsun
- T=3000 to >50,0000 K
- R=0.1 to 10 Rsun
Giants & Supergiants
There are also two bands of stars in the H-R diagram that are
brighter than Main Sequence stars with the same
effective temperatures.
The Luminosity-Radius-Temperature relation tells us that the stars in
these bands must therefore be larger in radius than Main Sequence
stars.
There are two groups of giant stars:
- Giants
- Large but cool stars with a wide range of luminosities:
- R = 10 to 100 Rsun
- L = 103 to 105 Lsun
- Supergiants
- The very largest stars, arranged along the top of the H-R diagram
with a wide range of effective temperatures but relatively
narrow range of luminosities:
- R > 103 Rsun
- L = 105 to 106 Lsun
White Dwarfs
There are also a few very hot but also very faint stars that occupy the
lower left-hand corner of the H-R Diagram. These are stars that are
much fainter than Main Sequence stars of the same
Temperature.
The Luminosity-Radius-Temperature relation tells us that these stars
must therefore be smaller in radius than Main Sequence stars.
How small? Using the Luminosity-Radius-Temperature relation, we can
make a prediction:
This is about the size of the Earth!
These stars are called White Dwarfs. "White" because they
tend to be very hot ("white hot"), and "Dwarfs" because they are so
tiny.
Luminosity Classification
Recall back in Lecture 9 we introduced the
M-K luminosity classes of stars, but didn't explain them.
Luminosity classification is based upon the widths of the
absorption lines in the star's spectrum.
It works because absorption lines are Pressure-sensitive:
- Lines get broader as the pressure increases.
- Big stars are puffier, which means the pressure in their
atmosphere is lower.
Implications:
- Larger stars have narrower absorption lines.
- Larger stars are brighter at the same
temperature.
Since larger stars are brighter at a given stellar temperature
(more surface area to radiate), measuring differences in the line widths
for stars of the same temperature gives an estimate of the
stellar luminosity.
This gives us a way to assign a relative Luminosity to
stars based upon their spectral line properties!
Locating stars on the H-R Diagram
Back in Lecture 9 I gave the M-K spectral
types of some familiar stars:
- The Sun: G2v (G2 Main-Sequence star)
- Betelgeuse: M2Ib (M2 Supergiant star)
- Rigel: B8Ia (B8 Bright Supergiant star)
- Sirius: A1v (A1 Main-Sequence star)
- Aldebaran: K5III (K5 Giant star)
The full spectral classification of a star tells us the approximate
location of the star on the H-R Diagram:
- The spectral class gives the star's relative temperature, hence
its horizontal location in the H-R Diagram.
- The luminosity class gives the star's relative luminosity at a given
temperature, hence its vertical location in the H-R diagram.
Questions:
The details of the H-R Diagram raise a number of questions. In
particular:
- Why don't stars have just any Luminosity or Temperature?
- Why is there such a distinct Main Sequence of stars? What
makes one Main Sequence star different from another?
- Were Giant, Supergiant, and White Dwarf stars born that way,
or is something else going on?
The answers to these questions forms the basis of the next unit of this
course, namely the internal structure and evolution of the stars.
The H-R diagram will prove to be one of our most powerful tools for
unravelling the mystery of the stars.
Supplement:
The Hipparcos H-R Diagram of the Solar Neighborhood
The key to making an H-R diagram of the nearest stars is being able to
measure accurate distances. These, combined with the measured apparent
magnitudes, allow us to compute the Luminosities of the stars.
The Hipparcos
satellite has made the most precise measurements of stellar
parallaxes to date for nearby stars. Using data for 4907 stars with
distances measured to better than 5% accuracy, this H-R Diagram for the Solar
Neighborhood has been made
[originals]. Because the points for many stars will
overlap each other in the plot, the Hipparcos team uses colors to show
how many stars sit under a single point. Red means more than 10 stars
at the place on the plot.
This remarkable H-R diagram has the following notable features:
- Most nearby stars (~85%) lie along the Main Sequence, as advertised.
Why this is true is an important clue to the nature of stellar
evolution.
- There are few if any Supergiants in the Solar Neighborhood. In
later lectures we'll learn why Supergiant stars are so rare.
- There are also very few White Dwarfs on this diagram. This time,
however, it is not a profound new result, but rather it is an artifact
of how the data were collected! White dwarf stars are intrinsically
very faint, but Hipparcos could only measure good quality parallaxes for
brighter stars. This particular H-R diagram uses only the 4907 best
parallaxes measured by Hipparcos, and so it excludes the many faint
white dwarf stars with poorer-quality parallaxes; only a handful of
white dwarfs are close enough, and hence bright enough, to yield 5%
accuracy parallaxes. This is an example of what we call a "selection
effect". We'll be meeting selection effects in various places during
the quarter.
Return to [
Unit 1 Index
|
Astronomy 162 Main Page
]
Updated: 2008 May 3
Copyright © Richard W. Pogge,
All Rights Reserved.