Data Source: IERS Rapid Service/Prediction Center, file "finals.all"
2002 January 25 at 12:15pm EDT
This is divided into three distinct parts:

Data Source: IERS Rapid Service/Prediction Center, file "finals.all"
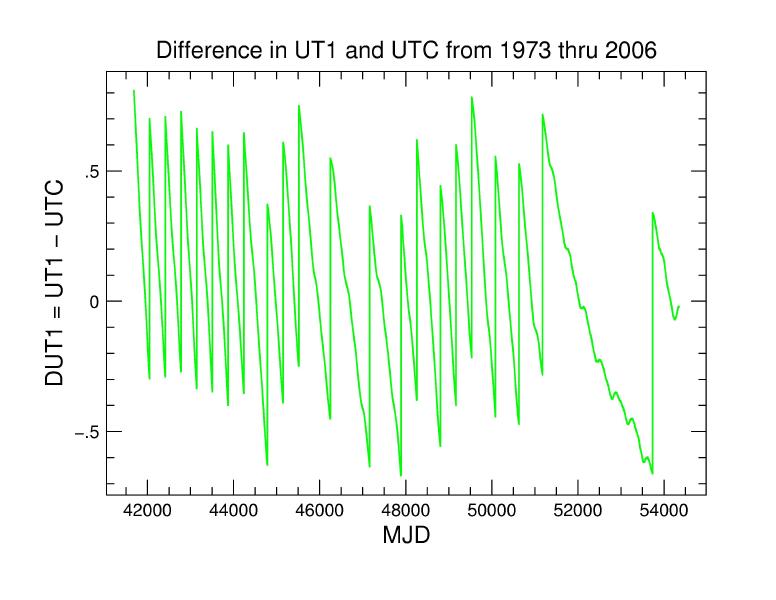
The big jumps in the figure above are the insertion of leap seconds.
The bottom line is that in astronomical research publications you should always use UTC if refering to observational data acquired after 1961, and UT for data acquired before.
So what about GMT?
Greenwich Mean Time (GMT) was replaced by UTC on 1972 January 1, and GMT proper is now more correctly UT1 (see above). However, in colloquial usage GMT is still incorrectly used the common name for the zone time in the UK during the winter months. More correctly the British Isles are on Western European Time (WET) in the winter, and Western European Summer Time (WEST), popularly known as British Summer Time (BST), in the summer. Further, the Greenwich Meridian is no longer the Prime Meridian as the International Prime Meridian is now located approximately 5-arcsec of longitude East (close, but not Greenwich).
In general, the term GMT must never to be used to denote "universal time". UTC is the only correct nomenclature.
Other Forms of Universal Time
There are two other forms of Universal Time you are unlikely to encounter unless you dig into some very technical literature. UT1R is a filtered version of UT1 that takes into account polar motions on shorter timescales to avoid some of the fine-grained jumps in conventional UT1. UT2 is a rarely used "smooth" version of UT1 that applies reasonably predictable periodic seasonal corrections to UT1.
UTC is measured by correcting TAI by an integer number of leap seconds to account for the changes in the Earth's rotation rate. Thus TAI is essentially "UTC without the leap seconds". The last leap second was inserted on 2005 December 31, so that since that date the offset between UTC and TAI is 33 seconds, hence:
UTC = TAI - 33s
That is, TAI is currently "ahead of" UTC by 33 seconds.
UTC was introduced in 1961. Between 1961 and 1971, UTC attempted to track changes in the Earth's rotation rate by introducing "elastic seconds", wherein the carrier frequency and tick duration of time signal radio broadcasts was adjusted annually to estimate how fast the Earth would rotate during that year. The accumulated discrepacies between this best guess and the actual measurements were corrected for in small steps of 50 to 100 msec that were applied annually. This system was a codification of schemes which had already been in use by various national laboratories and their radio broadcast time signal services for a number of years. Thus, UTC is "Coordinated" in the sense that the correction steps were determined and implemented by international agreement, instead of locally.
In 1972, an arguably simplified method was introduced whereby while leap seconds would be introduced more or less annually to take into account changes in the rotation rate of the Earth. This method is the one described above. Some in the IAU argued at the time that it should no longer be called "UTC" because of the considerable change in the rotation-correction algorithm, but in the end UTC it remains to this day. Thus far, leap seconds have always been positive, but there is no reason negative leap seconds won't be required in the future as the change in the Earth's rotation is not monotonic.
2002 January 25 January 25, 2002 1/25/2002 1/25/00 2002/25/1 2002-01-25and so forth. The first two are fine for English-language text, but they are inadequate for numerically coding data. The various numerical versions above are just a sampling of the different ways of writing down dates, all of which are prone to a bothersome "month number/day number" ambiguity. For example, does this date
3/6/33mean 1933 March 6, 1933 June 3, or 2033 March 6, etc.? The month/day numbers are ambiguous, and there is an additional ambiguity on the year in the form of the so-called "Y2K" problem.
To impose some order on the problem, the International Organization for Standardization (ISO) has introduced a standard notation for the expression of dates and times called ISO-8601. This standard specifies that calendar dates are expressed in terms of year, month, and day of month in that order, and times are expressed in the 24-hour timekeeping system. Widespread adoption of this standard should eliminate any day/month ambiguity, and explictly eliminates the Y2K problem for the expression of years.
Use of ISO-8601 date and time notation has been formally adopted by the IAU for all astronomical applications. It has also been adopted by the UN, all international space and aerospace consortia, and all telecommunications standards group. All scientists should adopt the ISO-8601 format, and forego use of any other date/time notation in their work.
Calendar dates are written as follows in ISO-8601 format:
ccyy-mm-ddwhere
ccyy = year, including the century year (e.g., 1961, 2001, etc.)
mm = month number (01..12)
dd = day number (01..31)
A full ISO-8601 date specification can include the time, for example:
2002-09-25T12:14:13.123ZWhere the T separates the date and time "fields", and the terminal Z indicates the timezone (here "Z" is "Zulu" or UTC). This is fine for computers, but many people find it awkward for everyday use.
Note that ISO-8601 only specifies the format for numerical respresentations, and does not cover language-dependent date notations. It is, however, a good idea in scientific writing to adopt a notation that uses the same basic ordering of elements as the numerical form. Thus, one would write calendar dates as
ccyy monthname ddFor example
2002 January 25in English. If you were writing in a different language, you would substitute the appropriate month name in that language, thus
2002 Enero 25in Spanish.
This date specification, however, is also incomplete. In scientific papers or data files, it is a good practice always explicity state the time system being used, thus
UTC 2002 January 25Without the explicit reference to the UTC system, you would have to either guess or (correctly or incorrectly) try to use knowledge of the observing location to which the date refers. Specifying the time system costs little in effort, but greatly relieves potential confusion.
The Julian Day number (JD) is the count of the number days that have elapsed since Greenwich Mean Noon on 1 January -4712 (4713 BC) in the Julian Proleptic Calendar. Julian Days start at noon, unlike UTC Gregorian Calendar days which start at midnight. The somewhat unusual starting date derives from the Julian Period of 7980 Julian Years of 365.25 days each. The Julian Period is the time interval between coincidences of the 28-year Solar Cycle, the 19-year Lunar Cycle, and the 15-year Roman Indiction (a tax cycle). The starting date is the last time all three cycles were coincident. This system provides astronomers with a way to measure secular time differences over long time spans without having to be concerned with getting the vagaries of the calendar correct.
An alternative to JD is the Modified Julian Date (MJD), an abbreviated, 5-digit version of the Julian Date defined as:
MJD = JD - 2400000.5
where 0.5 days is subtracted so as to have MJD start a midnight (i.e.,
aligning it with the civil time reckoning convention), and the 2400000
is used to reduce the 7-digit day number of JD to a more tractable 5
digits. This definition of MJD is officially recognized by the IAU, the
ITU (International Telecommunications Union), and the CCIR (Consultative
Committee for Radio).
In practice, both JD and MJD should be referenced to UTC, and in most astronomical research papers where it is not stated explicitly it is usually a safe assumption that UTC is implicit. However, there is no explicit mandate from the IAU (or anyone else) to define JD and MJD in terms of UTC, so it is a good idea to state your time system explicitly when using it in research publications or in data sets made available to others.
One often encounters a 4-digit version of the Modified Julian Date computed relative to JD2450000.0 instead of the internationally mandated JD2400000.5. This non-standard practice has been formally deprecated by the IAU and other international time-keeping organizations, and should not be used. Similarly there are other, even more idiosyncratic definitions of MJD in use, and you should not use any of those, either.
A more accurate way to express this is relative to the dynamical center-of-mass ("barycenter") of the Solar System, since the Sun also moves relative to the barycenter. In fact, use of HJD is formally deprecated by the IAU. Despite this, HJD continues to be common in the literature, while one rarely encounters a Barycentric Julian Date or its equivalent outside of fairly specialized papers. Why? One practical reason is that the relevant time systems for use in a Barycentric correction are not simply related to UTC and related terrestrial time systems. The calculation is non-trivial, and it does not help matters that the IAU has not followed up its deprecation of HJD with a set of standardized, portable, robust, and readily available algorithms for accomplishing the conversion. It also does not help that the relevant literature is nearly impenetrable to all but specialists, reflecting both the considerable technical complexities of the problem and the deep philosophical and political divisions prevailing among those working on time systems.
GPS offers two modes:
Differential GPS (DGPS) methods are employed when higher positional precision is required. Applications of DGPS include safety-critical navigation (ships and aircraft), precision surveying, and geodynamics work. If you can wait to make multiple measurements, sub-meter (centimeter or even millimeter) precision is achievable using linked receivers and sophisticated statistical analysis methods (the OSU Center for Mapping is the local expert on DGPS methods).
However, care must be taken when using GPS as an astronomical time reference. Unlike UTC, GPS is NOT adjusted for leap seconds. GPS time was last synchronized with UTC on 1980 January 6, and as of 2006 January 01, GPS is ahead of UTC by 14 seconds. Each GPS satellite transmits the UTC correction parameters as part of the navigational data stream, and most good GPS receivers include software to make the conversion for you transparently. Care should be taken to verify that you are indeed reading the UTC time and not the GPS time when you query your GPS receiver for "the time".
This page kept by UCO/Lick Observatory's Steve Allen provides a wealth of information about various time systems current and historical: