Determining the distance to celestial objects is a recurring theme in astronomy. Distances with the solar system are very well determined using radar techniques. For instance, the length of the astronomical unit (the mean distance between the Earth and Sun) has been measured to be 1 AU = 149,597,870.61 +/- 0.02 kilometers (an error of only 1 part in 7 billion). Radar is not useful beyond a range of 10 AU or so.
To determine stellar distances, the most useful tool is trigonometric parallax.
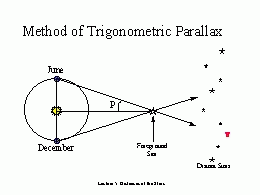
In the above diagram (click on the image for a larger version),
the angle p represents the
parallactic displacement (called ``parallax'' for short).
Over the course of a year, the image of the star moves in
an ellipse whose major axis has an angular length 2p.
After the angle p has been measured, the distance d
can be computed:
d = 1 AU / p ,
where p is given in radians. Since p
is a small angle, it's more convenient to measure it in
arcseconds, where 1 radian = 206,000 arcseconds, in round
numbers. If a star is at a distance of 206,000 AU, it
will have a parallax p of one arcsecond.
This distance is referred to as 1 parsec (pc).
1 parsec = 206,000 AU = 3.26 light years = 3.09 X 1016 meters
The nearest stars to us (other than the Sun) are the three stars of the Alpha Centauri system. The nearest of the three, called Alpha Centauri C, or Proxima Centauri, has a parallax p = 0.7723 +/- 0.0024 arcsec, and hence is at a distance d = 1/p = 1.295 +/- 0.004 parsecs (267,000 AU). The two other stars in the Alpha Cen system form a tightly bound binary with a parallax p = 0.7421 +/- 0.0014 arcsec; they are thus at a distance d = 1/p = 1.348 +/- 0.003 parsecs.
The best available parallax measurements were provided by the Hipparcos satellite, which measured parallaxes with a typical error of 0.001 arcsec. The Hipparcos satellite gave parallaxes for
If stars were all the same luminosity (or wattage), then the stars which appeared brightest would be the ones closest to us. However, as shown in Appendix 4 of the text, the nearest stars (as determined by parallax measurements) are not necessarily the brightest. Proxima Centauri is invisible to the naked eye, despite being only 1.3 parsecs away. Rigel ranks among the top ten brightest stars, despite being 250 parsecs away, nearly 200 times the distance to Proxima Centauri.
Intrinsic brightness is given by a star's luminosity, measured in watts. The luminosity of the sun is L = 3.86 X 1026 watts; this includes all the energy carried away by all the photons which the Sun emits.
Apparent brightness is given by a star's flux,
measured in watts per square meter. Consider a sphere of radius
d centered on a star of luminosity L.
The flux of light through the sphere is:
f = L / ( 4 pi d2 )
As an example, the Sun's flux at the Earth's location is
1370 W/m2.
If we can measure the flux from a distant star, and we know its distance, we can compute its luminosity. For instance, the flux of Sirius is f = 10-7 W/m2. Its distance, determined from its parallax, is d = 2.65 pc. By a simple calculation, we find that the luminosity of Sirius is L = 4 pi d2 f = 8 X 1027 watts, about 20 times the Sun's luminosity.
The first attempt to quantify flux was made by the ancient Greek astronomer Hipparchus. The brightest stars he could see were 1st magnitude (m = 1), the next brightest were 2nd magnitude (m = 2), and so forth, down to the faintest stars he could see, which were stars of the 6th magnitude (m = 6). After the invention of the telescope, the apparent magnitude system was extended to lower magnitudes (m = 7, 8, 9, and so forth) and to fractional magnitudes.
In the 19th century, it was realized that a difference
of 5 magnitudes corresponds to a multiplicative factor
of 100 in flux. Consider two stars with apparent magnitude
m1 and m2 and with corresponding
fluxes f1 and f2.
If m2 - m1 = 5, then
f1/f2 = 100.
If m2 - m1 = 1, then
f1/f2 = 1001/5 = 100.4 = 2.512.
In general,
f1 / f2 = 100.4(m2-m1).
This means that the apparent magnitude m is a logarithmic
measure of the flux f:
m = C - 2.5 log f ,
where the normalization constant C is chosen,
for esoteric historical reasons,
so that the star Vega has an apparent magnitude m = 0.
Since flux depends on both luminosity and distance, the
apparent magnitude depends on both luminosity and distance.
The absolute magnitude M of a star is
a logarithmic measure of its luminosity. The absolute
magnitude of a star is defined as the apparent magnitude
it would have if it were at a distance d = 10 parsecs.
(The reference distance of 10 parsecs is chosen for
esoteric historical reasons.)
m = C - 2.5 log f = C - 2.5 log L + 2.5 log (4 pi) + 5 log d
M = C - 2.5 log L + 2.5 log (4 pi) + 5
The difference between the apparent and absolute magnitude of
a star is called its distance modulus since
it is a logarithmic measure of its distance:
m - M = 5 log d - 5 ,
where the distance d is measured in parsecs.
Measuring a star's total (or `bolometric') flux is extraordinarily difficult. If stars were monochromatic, it would be easier, but the different wavelengths at which a star emits light require different detector technologies. It is much easier to measure the flux over a limited wavelength range. (Your eyes, for instance, measure flux over the wavelength range 400 nanometers to 700 nanometers. For bees, the relevant range is 300 to 550 nanometers...)
Compared to measuring a bolometric flux, it's much easier to measure flux over a limited wavelength range. This is done, in practice, by putting a filter in the light path of your telescope. Many different filter systems are in use; the example used in the textbook is the Johnson system (devised by H. L. Johnson and his collaborators starting in the 1950s). The B filter in the Johnson system, for instance, is centered at an effective wavelength of 440 nanometers and has a bandpass of 100 nm (`B' stands for Blue). The V filter is centered at a wavelength of 550 nanometers and has a bandpass of 90 nm (`V' stands for Visual). Other Johnson filters are U (for Ultraviolet), R (for Red) and I (for Infrared).
The flux of light making its way through the colored filter
can be converted to magnitudes. Using the V filter:
mV = CV - 2.5 log fV.
Using the B filter:
mB = CB - 2.5 log fB,
and so forth. Historically, the normalization of the magnitude
scale has been chosen so that the apparent magnitude of Vega
is m = 0 for each of the photometric bands U, B, V, R, and I.
Multicolor photometry (taking snapshots with a succession
of different filters) is useful because it permits, with a
minimum of effort, a reasonable estimate of a star's effective
temperature and apparent bolometric magnitude. The color
index of a star is the difference in its apparent magnitude
at two different effective wavelengths. One useful
color index is:
B - V = mB - mV = MB - MV.
Other frequently used color indices are U-B and V-R. The convention
for a color index is that it is always m(short wavelength) -
m(long wavelength).
The color index depends on a star's temperature. By definition,
Vega has B-V = 0. The effective temperature of Vega is approximately
10,000 Kelvin. If T > 10,000 K, then the star is bluer than
Vega (B flux enhanced relative to V flux), and hence B-V < 0.
If T < 10,000 K, then the star is redder than Vega (V flux
enhanced relative to B flux), and hence B-V > 0. For blackbodies,
a useful relation between temperature and B-V color index is:
B-V = -0.71 + 7090/T.
(More accurate conversions between B-V and T are found empirically.)
BOTTOM LINE: Measuring a color index such as B-V is a cheap and
quick way of estimating a star's effective temperature (lots easier
than taking a spectrum!)
Warning! Warning! In the real universe, you must take the effect
of extinction into account. Atmospheric extinction (due to the
Earth's atmosphere) causes about 0.2 magnitudes of V-band dimming when
your telescope is pointed straight up. For zenith angles less than
60 degrees, a useful approximation is
mV (above atmosphere) = mV(observed) - 0.2
sec z
where z is the zenith angle. Interstellar extinction,
caused by the interstellar medium, can also be significant, particularly
close to the midplane of our galaxy, where most of the interstellar
dust lies.
Since apparent bolometric magnitudes are difficult to measure, it
is useful to have a way of converting (at least approximately) from
V-band magnitudes to bolometric magnitudes. The bolometric
correction for a star is defined as
BC = mbol - mV = Mbol - MV.
For the Sun, for instance, Mbol=4.74 and MV=4.83,
so BC = -0.09. A star's bolometric correction is primarily
dependent on its effective temperature. The bolometric correction
is smallest for stars with T = 6700 Kelvin, since these are the
stars whose emission peaks in the V band. For stars with T > 6700 K,
most of the energy escapes at shorter wavelengths; for stars
with T < 6700 K, most energy escapes at longer wavelengths.
Bolometric corrections for main sequence stars (like the Sun, Sirius,
and the stars of the Alpha Centauri system) are given in Appendix 4
of the textbook.
Let's work through an example of how color indices and bolometric corrections might work in reality. The star Epsilon Eridani has mV = 3.73 and mB = 4.61. Its color index is then B-V = 4.61-3.73 = 0.88. If we use the blackbody approximation, this corresponds to a temperature T = 7090/(0.88+0.71) = 4500 Kelvin. The more accurate empirical relation given in the text yields a higher effective temperature of T = 4900 K. The bolometric correction for a main sequence star of this effective temperature is BC = -0.32. The apparent bolometric magnitude of Epsilon Eridani is mbol = mV + BC = 3.73-0.32 = 3.41. The distance to Epsilon Eridani (from the Hipparcos satellite) is d = 3.218 parsecs, so the absolute bolometric magnitude is Mbol = mbol+ 5 log (10 pc/d) = 5.87, and the luminosity is L / LSun = = 100.4 (4.74 - Mbol) = 0.35.
For the Sun, it's easy. The distance is
d = 1 AU = 1.496 X 108 km ,
and the angular size is
alpha = 1919 arcsec = 9.304 X 10-3 rad .
The radius of the Sun can then be computed as
r = 696,000 km. Measuring the angular diameter of
the Sun - over half a degree - is easy. However, if
we were viewing the Sun from the Alpha Centauri system,
it would only be 7 milliarcseconds (mas) in diameter.
The star Betelgeuse has been directly imaged, using the Hubble Space Telescope. Its distance, from parallax, is d = 130 pc = 27,000,000 AU. Its angular size is alpha = 0.125 arcsec = 6.06 X 10-7 rad. The computed radius of Betelgeuse is then r = 8.2 AU (that's 1800 times the radius of the Sun).
Supergiants like Betelgeuse are rare. To determine the angular diameter of most stars, you need to use interferometric techniques.
To determine the mass of stars, we must make use of
Kepler's Third Law, as modified by
Isaac Newton:
(M1+M2) P2 = a3,
where M1 and M2 are the mass of
two stars in a binary system (measured in solar masses),
P is the orbital period of the binary system (measured
in years), and a is the semimajor axis of the
relative orbit of the stars (measured in AU).
Note that if two stars are orbiting their mutual center of mass, Kepler's Third Law tells us the sum of their masses. Binary star systems are common. Of the 39 stellar systems within 5 pc of us (including the Solar System), 23 are single stars, 13 are binaries, and 3 are triples. (Quadruple star systems are known as well...)
Binary star systems are classified according to the method used to discover them. Of the types mentioned in the textbook, the most interesting are:
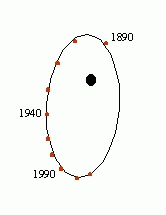
The orbital period of the Sirius system is P = 50.18 years.
The distance to the Sirius system is d = 2.637 pc = 544,000 AU.
The orbital inclination is i = 43.5 degrees.
The semimajor axis of the orbit of Sirius B relative to
Sirius B is a = 19.8 AU.
From Kepler's Third Law, the total mass of the Sirius system is:
MA + MB = a3/P2 =
3.08 Msun.
The ratio of the masses of Sirius A and Sirius B can be
found by finding the center of mass of the system. The
center of mass moves along a straight line as seen from
Earth, while Sirius A and Sirius B `wobble' to and fro
relative to the straight line motion. Let the distance
of Sirius A from the center of mass be aA
and the distance of Sirius B from the center of
mass be aB. Then MA/MB =
aB/aA. From inspection of the
motion of Sirius, aB/aA = 2.2.
The ratio of masses is thus MA/MB = 2.2.
Combined with the knowledge that MA + MB =
3.08 Msun, we compute:
MA = 2.12 Msun
MB = 0.98 Msun.
Sirius B is an example of a white dwarf;
an object as massive as the Sun, but smaller in volume
than the Earth.
Spectroscopic binaries are also useful. Consider the
case of two stars on circular orbits about their center of
mass. The orbital speed of each star is proportional to
the radius of its orbit:
vA = 2 pi aA / P
vB = 2 pi aB / P
Thus, Kepler's third law can be expressed in terms of the
orbital velocities, rather than the orbital radii:
MA + MB = ( P / 8 pi3 )
(vA + vB)3.
Unfortunately, we cannot measure vA and
vB; the Doppler shift that we measure only
tells us the orbital speed times the sine of the inclination
angle i. (Face-on orbit: i = 0. Edge-on orbit: i = 90 degrees.)
Thus, unless we know the inclination of a spectroscopic
binary, we can only measure its mass times the cube of
the sine of the inclination. However, if
a spectroscopic binary is also an eclipsing binary, we
know that its inclination is close to 90 degrees.
Most stars lie along a reasonably tight mass-radius relation. For stars with M < 1.3 Msun, M is proportional to r1.7. For more massive stars, M is linearly proportional to r. In addition, most stars lie along a tight mass-luminosity relation. For stars with M < 0.43 Msun, L is proportional to M2.3. For more massive stars, L is proportional to M4. This steep dependence of luminosity on mass implies that very massive stars are very short-lived, with lifetimes proportional to M-3.