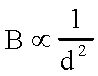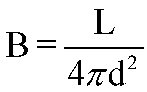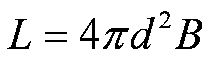|
Astronomy 162:
Introduction to Stars, Galaxies, & the Universe
Prof. Richard Pogge, MTWThF 9:30
|
Lecture 7: "Starlight, Starbright"
Stellar Brightness
Readings: Chapter 9, Section 19-2 & 19-3
- Luminosity of a star:
- total energy output
- independent of distance
- Apparent Brightness of a star depends upon
- distance
- luminosity
- Photometry & Stellar Magnitudes
How "Bright" is a Star?
There are two ways to answer the question of how bright a star
is quantitatively:
- Intrinsic Luminosity:
- Measures the Total Energy Output by the star in Watts
- Distance Independent (it is a physical property of the star itself)
Apparent Brightness:
- Measures how bright the star appears to be as seen from a distance.
- Depends on the distance to the star
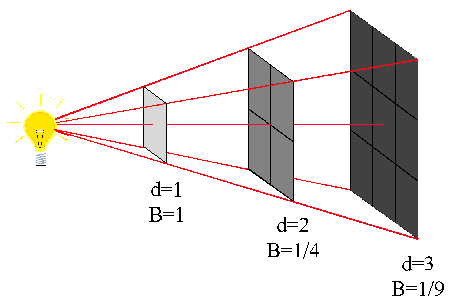
Inverse Square Law of Brightness
The Apparent Brightness of a source is a consequence of geometry. As
light rays emerge from a source, they spread out in area:
- Expressed mathematically:
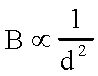
- In words:
- The Apparent Brightness (B) of a source is inversely proportional to the
square of its distance (d):
Implications:
For a light source of a given Luminosity...
- Closer = Brighter
- Move 2x closer to a light source
- It will appear 22=4 times brighter.
- Farther = Fainter
- Move 2x further away from a light source
- It will appear 22=4 times fainter
Apparent Brightness of Stars
How bright a star appears to be will depend upon:
- How bright it is physically (Luminosity)
- How far away it is (Distance).
These are related through the inverse square law of brightness
described above.
Brightness-Luminosity Relationship:
This relates the Apparent Brightness of a star (or other light source)
to its Luminosity (Intrinsic Brightness) through the
Inverse Square Law of
Brightness:
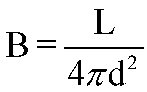
At a particular Luminosity, the more distant an object is, the fainter its
apparent brightness becomes as the square of the distance.
Appearances can be deceiving...
Does a star look "bright" because
- it is intrinsically very luminous?
- it is intrinsically faint but located nearby?
To know for sure, you must know either
- the distance to the star, or
- some other, distance-independent property of the star
that clues you in.
Measuring Apparent Brightness
The process of measuring the apparent brightnesses of objects is called
Photometry.
Two ways to express apparent brightness:
- Stellar Magnitudes
- Absolute Fluxes (energy per second per area)
Both are used interchangeably by astronomers.
Magnitude System
Traditional system dating from classical times, invented by Hipparchus of
Nicaea, c. 300BC.
Rank stars into "magitudes": 1st, 2nd, 3rd, etc., as follows:
- 1st magnitude stars are brightest stars,
- 2nd magnitude stars are the second brightest,
- and so forth...
- The faintest stars visible to the naked eye are 6th magnitude.
As originally applied by Hipparcus and others, this was a qualitative
ranking, as they had no reasonable means of independently measuring
brightnesses other than comparing them by-eye to other stars in the sky.
Magnitudes defined this way are measures of the relative brightnesses
of stars.
Modern Magnitude System
The modern system of magnitudes defines them as follows:
- 5 steps of magnitude = factor of 100 in brightness
- Bigger magnitude = fainter star.
- The standard of brightness is the star Vega (0th magnitude)
Examples:
- 10th mag star is 100x fainter than a 5th mag star.
- 20th mag star is 10,000x fainter than a 10th mag star.
- Faintest stars measured this far are ~30th magnitude.
Magnitudes are computationally very convenient to use, but the are
somewhat obtusely defined (it is backwards: larger magnitudes = fainter
stars).
Unlike the qualitative system of Hipparchus, the modern magnitude system
defines the standard of brightness as the bright star Vega (brightest
star in the summer constellation of Lyra), and precisely defines the
interval of magnitude. This quantification was done in the 19th century
and refined throughout the 20th century.
Flux Photometry
Count the photons received from a star using a light-sensitive
detector:
- Photographic Plates (old-school: 1880s to 1960s)
- Photoelectric Photometer (photomultiplier tube: 1930s to 1990s)
- Solid State Detector (e.g., photodiodes or CCDs)
We now use solid-state detectors like CCDs and similar technologies
(with very rare exceptions), as these detectors are far more sensitive
and stable than any previous technology.
Calibrate the detector by observing a set of "Standard
Stars" of known brightness.
Measuring Luminosity
To measure the Luminosity of a star you need 2 measurements:
- the Apparent Brightness (flux) measured via photometry, and
- the Distance to the star measured in some way
Together with the inverse square law of brightness, you can compute
the Luminosity as
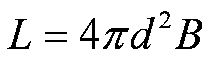
The biggest source of difficulty, as usual in Astronomy, is measuring
the distance accurately...
Practical Issues
In practice, we can use sensitive electronic instruments and photometry
to measure the apparent brightnesses of many hundreds of millions of
stars.
But, we have good distances (parallaxes) for only about 100,000 stars.
- Only that number of stars have direct estimates of their Luminosities.
- Since Luminosity depends on distance squared, small errors in
distance are effectively doubled (a 10% distance gives a 20%
luminosity).
Luminosity is an important quantity for understanding how stars work, and
measuring it with accuracy is still a practical issue even in 21st-century
astronomy.
Return to [
Unit 1 Index
|
Astronomy 162 Main Page
]
Updated: 2006 January 7
Copyright © Richard W. Pogge,
All Rights Reserved.