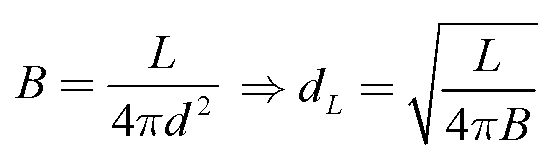|
Astronomy 162:
Introduction to Stars, Galaxies, & the Universe
Prof. Richard Pogge, MTWThF 9:30
|
Lecture 22: The Cosmic Distance Problem
Readings: Ch 26, section 26-4
- Geometric Distances
- Trigonometric Parallaxes
- Luminosity Distances
- "Standard Candles"
- Spectroscopic Parallaxes
- Cepheid Variables
- RR Lyrae Variables
The Distance Problem
Measuring accurate distances remains the biggest technical problem in
Astronomy.
Distances are necessary for estimating:
- The total energy released by objects (Luminosity)
- The physical sizes of objects
- The masses of objects
- The distribution of objects in space
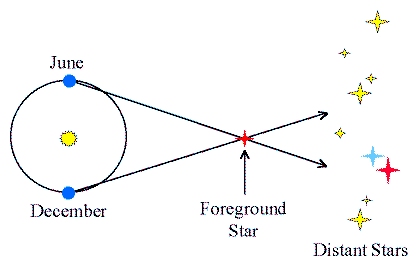
Geometric Distances
Direct measurements of distances using geometry.
Solar System Distances:
- Orbit Geometry (Copernicus)
- Radar Measurements
Stellar Distances:
(Click on the image to view at full scale [Size: 7Kb])
Parallax Limits
Ground-based parallaxes are measured to ~0.01-arcsec
- good distances out to 100 pc
- < 1000 stars this close
Hipparcos satellite measures parallaxes to ~0.001-arcsec
- good distances out to 1000 pc
- ~100,000 stars
Indirect distance estimate:
- Measure the object's Apparent Brightness, B
- Assume the object's Luminosity, L
- Solve for the object's Luminosity Distance, dL,
by applying the
Inverse Square Law of
Brightness
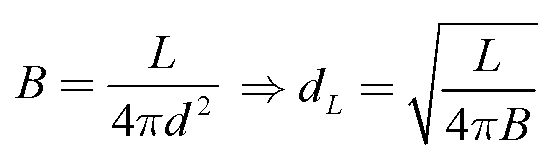
We call this the Luminosity Distance (dL) to distinguish
it from distances estimated by other means (e.g. geometric distances from
parallaxes).
The only observable is the object's Apparent Brightness, B. The
missing piece is the luminosity, (L), which must be inferred in some
way.
Any object whose Luminosity you know ahead of time ("a priori")
is known as a Standard Candle.
The way you establish that a class of objects is a standard candle is
via a multi-step calibration procedure known as the "Bootstrap Method".
Bootstrap Method:
- Calibrate the Luminosities of nearby objects for which
you have a Trigonometric Parallax distance.
- Identify distant but similar objects, using a
distance-independent property that they share.
- Assume that the distant objects have the same Luminosity
as the nearby objects for which you have distances.
Once you have a calibration of a set of standard candles, you can then
apply them to measuring distances to objects that are too far away for
geometric methods like parallaxes.
Distance-Independent Property:
- The observed spectrum of the star.
Physics:
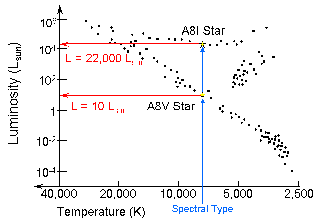
- The Spectral Type (OBAFGKML) tells you the star's Temperature.
- The Luminosity Class (I..V) tells you which region of the H-R Diagram
the star belongs in.
- Together, they give the star a unique location on a calibrated
H-R Diagram.
Method:
- Build up a calibrated H-R Diagram for nearby stars with good
parallax distances.
- Get Spectral Type & Luminosity Class of the distant star
from its spectrum.
- Locate the star in the calibrated H-R Diagram
- Read off the Luminosity
- Compute the Luminosity Distance (dL) from
is measured Apparent Brightness.
NOTE: Despite the name, the method has nothing to do with measuring
geometric "parallaxes".
Distance Limit:
- Practical limit few 100,000 pc.
- Works best for star clusters.
Problems:
- Luminosity Classes are only roughly defined.
- H-R diagram location depends on composition.
- Faint spectra give poor classifications.
While somewhat difficult to use accurately for individual stars, the
method of spectroscopic parallaxes works best for clusters of stars
where you can average over many measurements.
Periodic Variable Stars
Stars whose brightness varies regularly with a characteristic, periodic
(repeating) pattern.
Distance-Independent Property:
- Period (repetition time) of their cycle of brightness variations.
Physics:
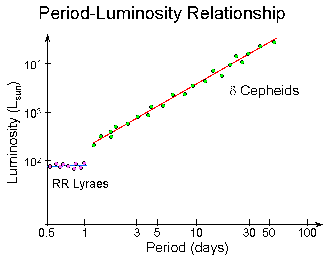
- Period-Luminosity Relations exist for certain classes
of periodic variable stars.
- Measuring the Period gives the Luminosity.
Class of rhythmically pulsating Supergiant stars:
- Found in young star clusters
- Luminosity of ~ 103-4 Lsun
- Brightness Range: few percent to a factor 2-3 in brightness
- Period Range: 1 day up to ~50 days.
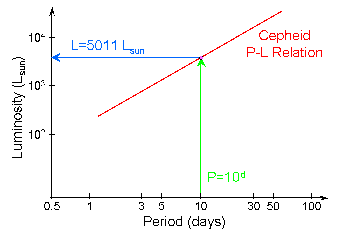
Period-Luminosity Relation:
- Longer Period = Higher Luminosity
- P = 3 days, L ~ 103 Lsun
- P = 30 days, L ~ 104 Lsun
Method:
- Measure the pulsation period (P)
- Using the P-L relation, read off the Luminosity (L)
- Compute the Luminosity Distance (dL) from the
Apparent Brightness and inferred Luminosity.
Distance Limit:
- 30-40 Megaparsecs (Hubble Space Telescope)
- Crucial for measuring distances to galaxies.
Problems:
- No Cepheids with precise parallaxes (a few now have low-quality
parallaxes measured by Hipparcos, but are just at the edge of
what Hipparcos can do).
- Two types of Cepheids with different P-L relations (delta Cephei and
W Virginis stars, respectively).
Despite the limitations and problems, Cepheid Variable Stars
(specifically delta Cephei stars) are one of the most important Standard
Candles we use to measure cosmic distances.
Rhythmically pulsating Horizontal-Branch stars:
- Found in old clusters, Galactic bulge & halo
- Luminosity of ~50 Lsun
- Brightness Range: factor of ~ 2-3
- Period Range: few hours to ~ 1 day.
- Relatives of Cepheid Variables
Period-Luminosity Relation:
- Less strong than for Cepheids
Method:
- Same as for Cepheids, but using the RR Lyrae P-L Relation to
get an estimate of the Luminosity.
Distance Limit:
- ~1 Megaparsec (Hubble)
- Limited to our Galaxy & Andromeda
Problems:
- No RR Lyrae stars with precision parallaxes
- RR Lyrae stars are fainter than Cepheids, so they are only
useful as standard candles relatively nearby.
The Cosmic Distance Scale
No single method will provide distances on all cosmic scales. Instead,
we have to rely on a multi-step approach that is carefully calibrated
at each step.
This makes the Cosmic Distance Scale look like a ladder with a series of
steps going from near to far:
- Calibrate Parallaxes using the Astronomical Unit (orbit of the Earth)
- Calibrate H-R diagram methods using stars with measured Parallaxes.
- Calibrate Cepheid and RR Lyrae star distances using H-R diagrams.
Inaccuracy and imprecision at each step carries forward into the next,
making each subsequent step less accurate.
Part of the challenge is to understand the sources of these inaccuracies
and taking them into account.
Return to [
Unit 4 Index
|
Astronomy 162 Main Page
]
Updated: 2006 February 5
Copyright © Richard W. Pogge, All Rights Reserved.