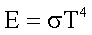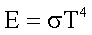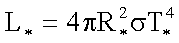Astronomy 162: Professor Barbara Ryden
Thursday, January 16
HOW BIG IS A STAR?
``The sun and the moon and the stars would have
disappeared long ago...had they happened to be
within the reach of predatory human hands.''
- Havelock Ellis
Key Concepts
- The radius of very few stars can be found from their angular
size and distance.
- The radius of other stars can be deduced from their
luminosity and temperature.
- Stars have a wide range of radii.
(1) The radius of very few stars can be found from their
angular size and distance.
The Sun's angular size is 1920 arcseconds (about half a degree,
or the size of your little fingernail held at arm's length).
Most stars are so far away from the Sun that their angular size
is not resolved, even in large telescopes. They are
indistinguishable from points of light.
Among the few stars that have been resolved is Betelgeuse.
The Hubble Space Telescope made a direct image
of the star Betelgeuse. The image has an angular size of only
0.125 arcseconds.
If the angular size `a' of a star and the distance `d' to that star
are known, then the radius `R' of the star can be computed.
For trigonometry fans only: the relevant equation is
R = d tan (a/2)
Astronomical applications
The Sun:
- a = 1920 arcseconds
- d = 1 AU = 150,000,000 kilometers
- We compute R = 700,000 kilometers
Betelgeuse:
- a = 0.125 arcseconds
- d = 427 light years = 4 thousand trillion kilometers
- We compute R = 1.2 BILLION kilometers
If the star Betelgeuse were superimposed on the Solar System, it would
stretch nearly as far as the orbit of Saturn.
(2) The radius of stars can be deduced from their
luminosity and temperature.
A star is approximately a blackbody. The luminosity of a blackbody
depends very strongly on temperature. Consider a square meter of
the surface of a blackbody. The rate at which it radiates light is
given by the following equation:
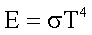
In the above equation, E is the luminosity of a square meter of the
blackbody's surface, the Greek letter sigma stands for a constant
which has been measured in the laboratory, and T is the temperature
of the blackbody's surface.
Double the temperature of a blackbody, and you increase its luminosity by
a factor of 2 x 2 x 2 x 2 = 16.
To find the total luminosity of a blackbody, multiply the luminosity
per square meter by the number of square meters on its surface. A star
is well approximated by a SPHERICAL blackbody (surface area = 4 pi R^2),
so the formula which gives the total luminosity of a star is the following:
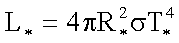
Thus, if we know the luminosity L* of a star (found from its intensity and
its distance) and if we know the temperature T* of a star, we can compute
its radius R*.
As an example, consider Sirius, the brightest star in the
night sky. It is actually a binary system. The more luminous
of the two stars in the system is called Sirius A; the
less luminous (which can only be seen in a
large telescope) is called Sirius B. Let's examine the two
stars in the Sirius system individually.
Sirius A:
- L = 26 Lsun
- T = 10,000 Kelvin = 1.72 Tsun
- R is computed to be 1.7 Rsun (Work this
out for yourself!)
Sirius B:
- L = 0.0024 Lsun
- T = 15,000 Kelvin = 2.59 Tsun
- R is computed to be 0.007 Rsun (Work this
out for yourself!)
One square meter of the companion of Sirius is 2.59 x 2.59 x 2.59
x 2.59 = 45 times more
luminous than one square meter of the Sun. The reason why the companion
to Sirius has such a low total luminosity is that it's tiny - even smaller
than the Earth.
(3) Stars have a wide range of radii.
- Betelgeuse = 1800 Rsun
- Sirius = 1.7 Rsun
- Sun = 1 Rsun , by definition
- Companion of Sirius = 0.007 Rsun
The largest known star has a radius 3700 times that of the Sun. On the
other hand, the objects known as `neutron stars' have radii of only 10
kilometers, although they are even more massive than the Sun.
Because the radius of Betelgeuse is larger than that of the
Sun by a factor of 1800, its volume is larger by a factor
of 18003 (about 6 billion). If the density of
Betelgeuse is comparable to that of the Sun, then its mass
is billions of times greater than that of the Sun. On the
other hand, if the mass of Betelgeuse is comparable to that
of the Sun, then its density is less than a billionth the
Sun's density. So which is it? Is Betelgeuse fat, or is it
just fluffy?
Prof. Barbara Ryden
(ryden@astronomy.ohio-state.edu)
Updated: 2003 Jan 16
Copyright © 2003, Barbara Ryden