The relation between the radial speed and distance of a galaxy is known as the Hubble Law, in honor of Edwin Hubble. In mathematical form, it can be written as:
Within our Solar System, distances to planets are found, with great accuracy, by using radar (radio signals bounced off planets). Unfortunately, radar is only useful out to a distance of approximately 10 AU; beyond that distance, the radio `echo' is too faint to detect.
Within our galaxy, distances to nearby planets are found using stellar parallax (described in the lecture for Monday, January 13. Unfortunately, stellar parallax is only useful out to a distance of approximately 500 parsecs; beyond that distance, a star's shift in position is too small to measure.
Distances between galaxies are typically measured in megaparsecs. One megaparsec (abbreviated Mpc) is equal to 1,000,000 parsecs, or 3,260,000 light years. At these distances, neither radar nor stellar parallax is useful. The distance of a galaxy (which may be many megaparsecs away) can be found if the galaxy contains a standard candle. A standard candle is an object whose luminosity L is known. The known luminosity, combined with the measured apparent brightness b for the object, gives us the distance. (The relation among luminosity, apparent brightness, and distance is given in the lecture for Tuesday, January 14, if you would like a review.)
The fundamental problem with standard candles is determining their luminosity in the first place. (After all, stars aren't labeled like lightbulbs!) If you knew the distance d as well as the apparent brightness b, you could compute the luminosity L of the standard candle. BUT the distance is just what we were trying to find! Thus, we seem to be stuck in a circular argument: ``In order to determine the distance, we need to know the distance in the first place.'' To avoid this circular argument, we need to build a ``distance ladder'', starting with nearby standard candles, with distances known from their parallax, and building outward to standard candles of unknown parallax. Steps in building a distance ladder:
Beyond 30 Mpc, however, Cepheids are too dim to be detected. At larger distances, we need brighter standard candles. Type Ia supernovae are superb standard candles. They are all basically the same (if you've seen one carbon-oxygen white dwarf explode, you've seen them all!) Thus, all Type Ia supernovae have about the same luminosity: L = 4 billion Lsun. Supernovae are 100,000 times more luminous than even the brightest Cepheid stars, and can be seen at distances of thousands of megaparsecs. The biggest problem with Type Ia supernovae is that they are infrequent. Even a large galaxy only has one supernova per century, on average.
A few nearby galaxies are found to be moving towards us. The
Andromeda Galaxy (M31), for instance, is
blueshifted. That is, the absorption lines in
its spectrum are shifted to shorter wavelengths, by
an amount z = -0.001. We deduce, therefore, that
our galaxy and the Andromeda Galaxy are moving toward
each other, with a relative speed
v = c z = (300,000 km/sec) (-0.001) = -300 km/sec.
(The negative speed implies that the distance between
the two galaxies is decreasing with time.) A
plausible explanation for this observation is that our galaxy
and the Andromeda Galaxy form a binary system, on elongated
orbits around their center of mass. The galaxies have recently
passed apocenter (the point of maximum separation) and are
now moving toward each other.
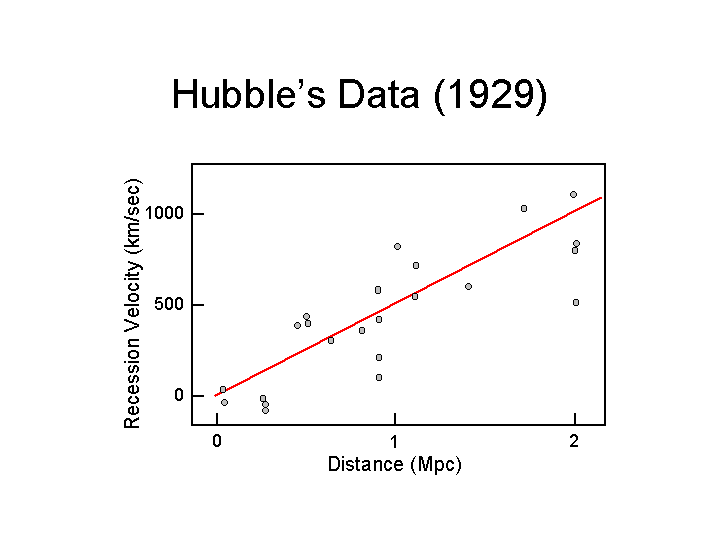
A VERY SURPRISING discovery was made in the early decades of this
century. Edwin Hubble discovered that galaxies more distant
than the Andromeda Galaxy are all
redshifted.
That is, they are all receding from us, moving steadily further away.
Moreover, the recession speed of a galaxy is proportional
to its distance: the farther a galaxy is from us, the faster
it's moving away:

The relation between the radial speed and distance of
a galaxy is known as the
Hubble Law, in honor of Edwin Hubble.
In mathematical form, it can be written as:
v = H0 d
where v is the radial speed of a galaxy (equal to its redshift times the speed of light), d is the distance to the galaxy, and H0 is a constant known as the Hubble constant. Ironically, Hubble himself badly overestimated the value of the Hubble constant (he thought that galaxies were closer than they actually are). The best current value of the Hubble constant is H0 = 70 km/sec/Mpc.
The Hubble Law is a surprising result. Why are galaxies flying away from us? Is it something we said? In fact, our galaxy does not possess a special repulsive force. Galaxies are receding, from our point of view, because the universe is EXPANDING. If we were located in ANY galaxy in the universe, distant galaxies would appear to be fleeing from us, due to the universal expansion (More on this subject later, when we talk about the Big Bang and the Expanding Universe.)
For our purposes at the moment, it suffices to point out that
the Hubble Law permits us to find distances to far-away galaxies.
Radial velocities are relatively easy to measure. Once we measure
v for a galaxy, we can compute
d = v / H0 .
For instance, suppose a galaxy is moving away from us at 14,000 km/sec.
Its distance, using the Hubble Law, is thus
d = (14,000 km/sec) / (70 km/sec/Mpc) = 200 Mpc.
The galaxy is 200 megaparsecs away (652 million light years), beyond
the region where Cepheids can be used to compute distances. The
major drawback to using the Hubble Law is that the value of H0
(the Hubble Constant) is poorly known.
Updated: 25 Feb 2003
Copyright © 2003, Barbara Ryden