Astronomy 161
Introduction to Solar System Astronomy
Prof. Paul Martini

Lecture 18: Resonances

Key Ideas:

Every object in the Solar System feels gravitational pulls from all of the other objects
Three-Body Problem: Lagrange Points; Earth-Moon and Sun-Jupiter Systems
Gravitational Interactions: Long-Range Perturbations (discovery of Neptune); Close Encounters (slingshot effect)
Resonances: Orbital (Mean-Motion) Resonances

Beyond Kepler

Newton's formulation of Kepler's Law only strictly applies to idealized systems with only 2 massive bodies orbiting each other
The Solar System is a "many-body" system: Eight planets; Multiple moon systems; Millions of small Asteroids and Icy Bodies; Lots of smaller debris (meteors and comets)
How can one calculate these effects?

The Three-Body Problem

What is the orbit of a small body in the combined gravitational field of two larger objects orbiting each other?: Spacecraft in the Earth-Moon System; Asteroid orbiting the Sun near Jupiter
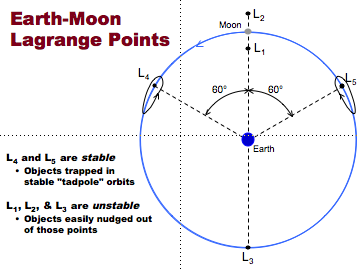
Solution by Joseph Lagrange (1736-1813): Solved the "Restricted" 3-body Problem; Found 5 "islands of equilibrium" that orbit in lock-step with the main 2 bodies
Lagrange Points: L1, L2, and L3 are unstable, while L4 and L5 are stable

Gravitational Interactions

To a first approximation, most orbits around the Sun are 2-body Keplerian orbits:: The Sun is ~1000x more massive than all the planets, moons, and small bodies combined; The Solar System is mostly empty, with large distances between big objects
Since gravity is an inverse-square law force:: Gravity from other bodies is much less than the Sun's gravity; But the effects can accumulate over time; Or can be large in close encounters

Long-Range Perturbations

Long-range interactions between two massive bodies orbiting the Sun
Extra gravitational forces accelerate the bodies relative to their Keplerian orbits:: "Perturbed" from simple Keplerian paths; Strongest when the two bodies are lined up at opposition (closest approach); Less massive objects experience stronger acceleration (a = F/m)
Effects accumulate over time, although in most cases they cancel out

The Discepant Orbit of Uranus

In 1781, William Herschel accidentally discovered the 7th planet Uranus
By 1840, the discrepancies between the predicted and actual positions of Uranus were larger than 1 arcminute: Perturbation was larger than predicted from the gravity of the known planets combined
This suggested the extra acceleration was from an 8th, unknown planet orbiting beyond Saturn.

The Discovery of Neptune

Calculations predicted the location of the new planet: Performed by Urban LeVerrier in France and John Couch Adams in England
1846 Sept 23: Galle in Berlind found Neptune only 52 arcminutes from the predicted spot!
This was another predictive triumph of Newtonian Gravity!

Close Encounters

Close encounters between objects have much stronger effects:: Dramatically alter orbits of one or both bodies; Smaller objects are more strongly affected
Examples: Comet perturbed into a new orbit after a close encounter with Jupiter; Gravity assist from Jupiter to accelerate a spacecraft into the outer Solar System; Gravity assists from the Earth and Venus to decelerate a spacecraft into the inner Solar System

Orbital Resonances

Small perturbations at opposition usually happen at different places along the orbit: Effects average out over long times
But, if the periods are whole-number ratios, get regular, periodic perturbations at the same place in the orbit: Repeated tugs add up over time; Regular close encounters destabilize orbits, but; If synchronization avoids close encounters, the orbit can stabilize

Naming Resonances

Named by the number of orbits completed by each body in the same time: First number = number of orbits completed by the dominant (most massive) body; Second number = number of orbits completed in the same time by the smaller body
Examples:: Pluto 3:2 resonance with Neptune (3 Neptune orbits for every 2 Pluto orbits); Asteroid Hilda in a 2:3 Resonance with Jupiter (2 Jupiter orbits for every 3 Hilda orbits)

Solar System Resonances

Main Asteroid Belt - Resonances with Jupiter: Kirkwood Gaps (unstable resonances); Asteroid Families (stable resonances); Trojan Asteroids - 1:1 resonance with Jupiter
Kuiper Belt resonances with Neptune: Pluto and Plutinos in 3:2 resonance orbits; Twotinos - objects in 2:1 resonance orbits
Jupiter and Saturn Systems: Jupiter: 1:2:4 Laplace Resonance of the moons Io, Europa, and Ganymede; Saturn: resonance moons and Ring gaps

Dynamical Evolution

The Solar System is not a static "clockwork": The dynamical state changes over time as the planets interact gravitationally
Resonances can amplify these effects:: Some resonant orbits are unstable and get depopulated; Others are stable and objects are swept into them where they form distinct dynamical families; Both have helped dynamically "shape" the Solar System over its long history

See A Note about Graphics to learn why some of the graphics shown in the lectures are not reproduced with these notes.