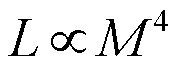Astronomy 1101 --- Plantes to Cosmos
Todd Thompson
Department of Astronomy
The Ohio State University
The Main Sequence
- Main Sequence stars are those that "burn" Hydrogen
into Helium in their cores.
- Get slowly brighter with age.
- The Main Sequence is a Mass Sequence:
- Lower M-S: M < 1.2 Msun
- Upper M-S: M > 1.2 Msun
- The Main-Sequence Lifetime depends on the Mass:
- Larger Mass = Shorter Lifetime
tnuc = f ε M c2 / L
tM-S ∝ 1/M3
L ∝ M4
Main Sequence Membership
For a star to be located on the Main Sequence in the H-R diagram:
- It must be in Hydrostatic Equilibrium (Pressure balances Gravity)
- It must be in Thermal Equilibrium (Energy Generation balances
Luminosity)
- It must generate energy by "burning" Hydrogen into Helium in its core.
Relax any of these conditions and the star must leave the Main Sequence.
Main Sequence stars are in Hydrostatic
Equilibrium (Thermal Pressure = Gravity).
This requires a high central Pressure.
Since we have an ideal gas, Pressure = Density x Temperature:
- Temperature: mean speeds of the nuclei
- Density: number of nuclei per cubic centimeter
As Hydrogen is fused into Helium in the core there are fewer nuclei
around (4 H become 1 He). As a consequence:
- The remaining nuclei must move faster to maintain the
same high Pressure as before.
- The gas at the center gets slowly hotter.
- This causes fusion to run faster as the temperature rises.
The result is that Main Sequence stars get slowly brighter as they age.
- It's a small effect: ~0.7% brighter every 100 Myr
We would not notice this on a human timescale, but there is evidence of
changes in the Sun's brightness over geologic time (specifically the Sun
has gotten about 30% brighter over the last 4.5Gyr since the formation
of the Earth).
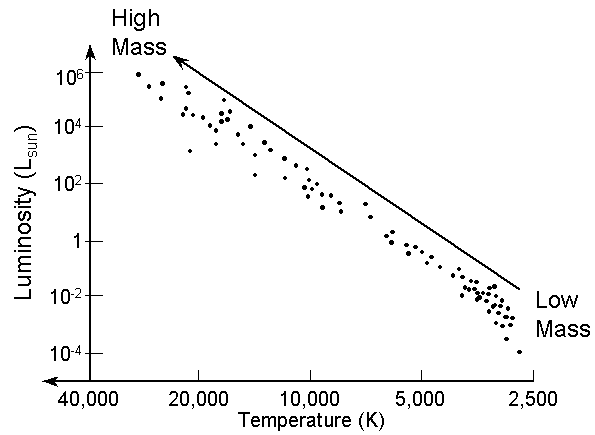
The Main Sequence is a Mass Sequence
The location of a star along the M-S is determined by its Mass.
- Low-Mass Stars: Cooler and Fainter
- High-Mass Stars: Hotter and Brighter
 (Graphic by R. Pogge)
(Graphic by R. Pogge)
Recall that M-S stars obey a strong Mass-Luminosity Relation:
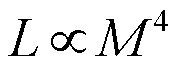
(Graphic by R. Pogge)
(In words: High-mass M-S stars are more luminous than low-mass
M-S stars proportional to the 4th power of their Mass.)
Internal Structure
Nuclear reaction rates are very sensitive to core temperature:
- P-P Chain : rate ~ T4
- CNO Cycle : rate ~ T18 !
The leads to:
- Differences in internal structure.
- Division into Upper and Lower Main-Sequences by mass.
The dividing line is at about 1.2 Msun, the mass at which the
P-P chain and CNO cycle both contribute equally to the total energy
generation in the core.
Upper Main Sequence
Upper Main-Sequence stars have
- M > 1.2 Msun
- TCore > 18 Million K
Hydrogen fusion occurs via the CNO Cycle.
- Internal Structure:
- Convective Core
- Radiative Envelope
[Schematic of an Upper M-S Star interior]
(Graphic by R. Pogge)
Lower Main Sequence
Lower Main-Sequence stars have
- M < 1.2 Msun
- TCore < 18 Million K
Hydrogen fusion occurs via the
Proton-Proton Chain
- Internal Structure:
- Radiative Core
- Convective Envelope
[Schematic of a Lower M-S Star interior]
(Graphic by R. Pogge)
The Lowest Mass Stars
Mass Range: 0.25 > M* > 0.08 Msun:
- Generate energy by the P-P Chain.
These stars have Fully Convective Interiors:
- Convective Core and
- Convective Envelope
Genericaly called Red Dwarf Stars
[Schematic of a red dwarf interior]
(Graphic by R. Pogge)
How long a star can continue to generate energy by fusing H into He in
its core depends upon how much fuel it has (total mass of the star),
and how fast it is burning it (luminosity).
We call this the Nuclear Timescale:
tnuc = f ε M c2 / L
where
- f = fraction of nuclear fuel available for fusion
- e = efficiency of matter-energy conversion
- M = mass of the star
- L = luminosity of the star
The nuclear timescale is just the amount of time it takes to burn
all of the nuclear fuel the star has, at its current luminosity.
For the Sun:
- tnuc = 10 Gyr given that f = 10% of the Sun's H is
available for fusion into He with a matter-energy conversion
efficiency of ε = 0.7%
Main Sequence Lifetime
The Nuclear Timescale above depends on the Mass (M)
and Luminosity (L). But, we know from the
Mass-Luminosity Relation for Main Sequence
Stars that
- L = M4
If we combine this with the formula for the Nuclear
Timescale, we get the Main Sequence Lifetime:
tMS ~ 1 / M3
In words, this equation means that more massive stars have
shorter Main Sequence lifetimes. Two stars that differ in
mass by a factor of 3, will have main-sequence lifetimes
that differ by a factor of 33 = 3 x 3 x 3 = 27.
The more massive star's main-sequence lifetime is nearly
30 times shorter than the less massive star's.
In summary:
- High-Mass M-S Stars have short M-S lifetimes
- Low-Mass M-S Stars have long M-S lifetimes
Examples:
- Sun:
- M = 1 Msun, and tMS = 10 Gyr
- Massive Star (10 Msun):
- tMS = 10 Gyr / (10 Msun)3 = 10 Million Years
- Low-Mass Star (0.1 Msun):
- tMS = 10 Gyr / (0.1 Msun)3 = 10 Trillion Years
Consequences:
Some observational consequences of the Main-Sequence lifetime
depending strongly on the Mass of the star:
- If you see an O or B dwarf star, it must be relatively young
as O and B stars evolve very rapidly and live for only a few Million
years.
- You can't tell how old an M dwarf is because their M-S lifetimes
are extremely long and they evolve very slowly.
- The Sun is ~5 Billion years old, so it will only last for about
another ~5 Billion years.
Updated/modified 2014, Todd Thompson
Copyright Richard W. Pogge,
All Rights Reserved.
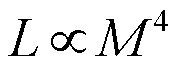
 (Graphic by R. Pogge)
(Graphic by R. Pogge)