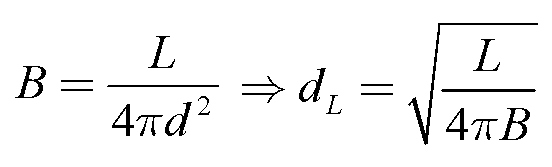Astronomy 1101

Astronomy 1101 --- Planets to Cosmos

Todd Thompson
Department of Astronomy
The Ohio State University

The Milky Way and Distances

Key Ideas

The Milky Way is our Galaxy: Diffuse band of light crossing the sky; Galileo: Milky Way consists of many faint stars
The Nature of the Milky Way: Philosophical Speculations: Wright & Kant; Star Counts: Herschels & Kapteyn; Globular Cluster Distribution: Shapley
Geometric Distances: Parallax
Luminosity Distances: "Standard Candles"; RR Lyrae Variables; Cepheid Variables

The Milky Way

Diffuse band of light crossing the night sky.

All human cultures have named it:

a Celestial River
a Celestial Road or Path

Our words "Galaxy" and "Milky Way" are derived from Greek and Latin:

Greek: Galaxias kuklos = "Milky Band"
Latin: Via Lactea = "Road of Milk"

"The Starry Messenger"

Galileo (1610):

Galileo observed the Milky Way with his new telescope.
Published his findings in his pamphlet, Siderius Nuncius (The Starry Messenger)

"For the Galaxy is nothing else than a congeries of innumerable stars distributed in clusters."

This was the first observation that showed that the Milky Way was simply made of many many unresolved faint stars.

Philosophical Interlude

Thomas Wright (1750):

Picture motivated by theological considerations
Wright made no new observations.

Model:

Milky Way is a thin spherical shell of stars.
The Sun is located inside the shell about midway between the inner and outer edges.

[Section of Wright's original woodcut]

(Graphic by R. Pogge) From our location near the Sun:

Looking along the shell: See a broad band of stars ("Milky Way")
Look out along the thin part of the shell: See few stars

A Theory of the Heavens

Immanuel Kant (1755):

Misread a newspaper account of Wright's model.
Also made no observations of his own.

Model:

Lens-shaped disk of stars rotating about its center.
No special place for the Sun.
Other "nebulae" are distant, rotating milky ways like ours.

Later became known as the "Island Universe" Hypothesis (term coined by Alexander von Humboldt, Kosmos, 1845).

The Herschels' Star Gauges

William & Caroline Herschel (1785):

Counted stars along 683 lines of sight using their 48-inch telescope.
Assumed that all stars are the same luminosity, so the relative brightness give relative distance.
Assumed that they could see all the way to the edges of the system.

Model:

Flattened Milky Way ("grindstone")
Sun located very near the center.

The Milky Way Map of William Herschel. Click to see a larger version.
Figure 4 from On the Construction of the Heavens by William Herschel, published in Philosophical Transactions of the Royal Society of London, Vol. 75 (1785), pp. 213-266. Image scanned by the author.

The Kapteyn Universe

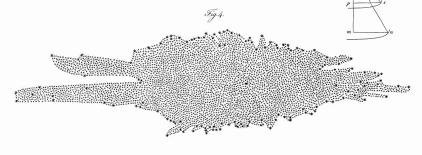
Jacobus Kapteyn (1901 thru 1922):

Used photographic star counts
Estimated distances statistically based on parallaxes & proper motions of nearby stars.
Neglected interstellar absorption of starlight (assumes that stars were faint only because they far away, not because interstellar absorption blocks some of the light).

Model:

Milky Way is a flattened disk ~15 kpc across & ~3 kpc thick
The Sun is located slightly off-center.

Sketch based on Kapteyn's paper.

(Graphic by R. Pogge)

Harlow Shapley (1915 thru 1921)

Astronomer at the Harvard College Observatory who was working on the nature of Globular Clusters of Stars.

Shapley noted two facts about Globular Clusters:

They were uniformly located above & below the Milky Way.
They were concentrated on the sky toward Sagittarius.

Observations:

Estimated Globular Cluster distances from observations of their RR Lyrae stars
Used these distances to map the globular cluster distribution in space.

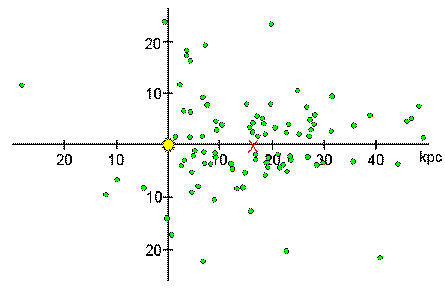
Sketch based on Shapley's original data, uncorrected for interstellar absorption. The Sun is located at the center of the axes (looking roughly side-on), and the center of the Milky Way inferred by Shapley is marked by the red X.

(Graphic by R. Pogge)

The Greater Milky Way

Shapley's Results (1921):

Globular clusters form a subsystem centered on the Milky Way.
The Sun is 16 kpc from the MW center.
MW is a flattened disk ~100 kpc across

Right basic result, but too big:

Shapley ignored interstellar absorption
Caused him to overestimate the distances.

The Problem of Absorption

Absorption of Starlight by Interstellar Dust:

Interstellar space is filled with gas and dust
This dust absorbs and scatters starlight passing through it,
This makes more distant objects look fainter than they otherwise would be if there were no interstellar dust.
If left unaccounted for, it can lead to serious overestimates of Luminosity Distances.

Absorption by Interstellar Dust affects all attempts to map the Milky Way:

Shapley & Kapteyn thought it was smaller than it actually is, and so overestimated the size of the Milky Way.
Robert Trumpler (1930) showed that interstellar dust absorption was significant.

The Milky Way

Our present view of the Milky Way today is largely Shapley's model, but corrected for the effects of interstellar absorption:

A flattened disk of stars with a central bulge.

[Credit: Two Micron All Sky Survey Project]
The Sun is located 8 kpc away from the Galactic Center, which is in the direction of the constellation of Sagittarius
The disk is ~30 kpc in diameter and ~1 kpc thick at the location of the Sun.

[Credit: Spitzer Science Center Illustration]
The Galactic Center and much of the disk of our Galaxy is obscured by interstellar dust in the plane of the Galaxy.

The Distance Problem

Measuring accurate distances remains the biggest technical problem in Astronomy.

Distances are necessary for estimating:

The total energy released by objects (Luminosity)
The physical sizes of objects
The masses of objects
The distribution of objects in space

Geometric Distances

Direct measurements of distances using geometry.

Stellar Distances:

Method of Trigonometric Parallax

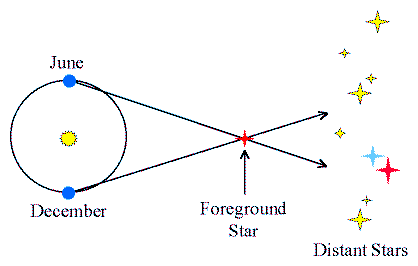
(Click on the image to view at full scale [Size: 7Kb]) (Graphic by R. Pogge)

Parallax Limits

Ground-based parallaxes are measured to ~0.01-arcsec

good distances out to 100 pc
< 1000 stars this close

Hipparcos satellite measures parallaxes to ~0.001-arcsec

good distances out to 1000 pc
~100,000 stars

Luminosity Distances

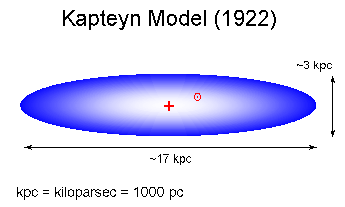
Indirect distance estimate:

Measure the object's Apparent Brightness, B
Assume the object's Luminosity, L
Solve for the object's Luminosity Distance, d_L, by applying the Inverse Square Law of Brightness

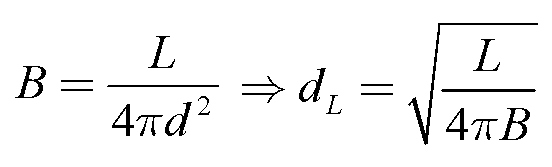
(Graphic by R. Pogge)

We call this the Luminosity Distance (d_L) to distinguish it from distances estimated by other means (e.g. geometric distances from parallaxes).

The only observable is the object's Apparent Brightness, B. The missing piece is the luminosity, (L), which must be inferred in some way.

Standard Candles

Any object whose Luminosity you know ahead of time ("a priori") is known as a Standard Candle.

The way you establish that a class of objects is a standard candle is via a multi-step calibration procedure known as the "Bootstrap Method".

Bootstrap Method:

Calibrate the Luminosities of nearby objects for which you have a Trigonometric Parallax distance.
Identify distant but similar objects, using a distance-independent property that they share.
Assume that the distant objects have the same Luminosity as the nearby objects for which you have distances.

Once you have a calibration of a set of standard candles, you can then apply them to measuring distances to objects that are too far away for geometric methods like parallaxes.

Periodic Variable Stars

Stars whose brightness varies regularly with a characteristic, periodic (repeating) pattern.

Distance-Independent Property:

Period (repetition time) of their cycle of brightness variations.

Physics:

Period-Luminosity Relations exist for certain classes of periodic variable stars.
Measuring the Period gives the Luminosity.

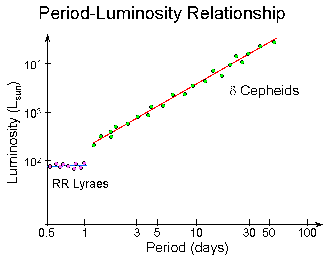
Schematic Period-Luminosity Relationship

(Graphic by R. Pogge)

RR Lyrae Variables

Rhythmically pulsating Horizontal-Branch stars:

Found in old clusters, Galactic bulge & halo
Luminosity of ~50 L_sun
Brightness Range: factor of ~ 2-3
Period Range: few hours to ~ 1 day.
Relatives of Cepheid Variables

Period-Luminosity Relation:

Less strong than for Cepheids

Method:

Same as for Cepheids, but using the RR Lyrae P-L Relation to get an estimate of the Luminosity.

Distance Limit:

~1 Megaparsec (Hubble)
Limited to our Galaxy & Andromeda

Problems:

No RR Lyrae stars with precision parallaxes
RR Lyrae stars are fainter than Cepheids, so they are only useful as standard candles relatively nearby.

Cepheid Variables

Class of rhythmically pulsating Supergiant stars:

Found in young star clusters
Luminosity of ~ 10^3-4 L_sun
Brightness Range: few percent to a factor 2-3 in brightness
Period Range: 1 day up to ~50 days.

Period-Luminosity Relation:

Longer Period = Higher Luminosity
P = 3 days, L ~ 10³ L_sun
P = 30 days, L ~ 10⁴ L_sun

Method:

Measure the pulsation period (P)
Using the P-L relation, read off the Luminosity (L)
Compute the Luminosity Distance (d_L) from the Apparent Brightness and inferred Luminosity.

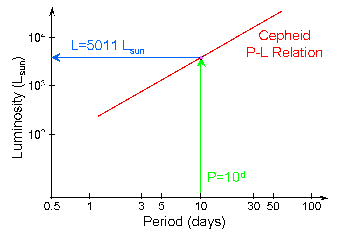
Cepheid P-L Relation Distance Determination

(Graphic by R. Pogge)

Distance Limit:

30-40 Megaparsecs (Hubble Space Telescope)
Crucial for measuring distances to galaxies.

Problems:

No Cepheids with precise parallaxes (a few now have low-quality parallaxes measured by Hipparcos, but are just at the edge of what Hipparcos can do).
Two types of Cepheids with different P-L relations (delta Cephei and W Virginis stars, respectively).

Despite the limitations and problems, Cepheid Variable Stars (specifically delta Cephei stars) are one of the most important Standard Candles we use to measure cosmic distances.

The Cosmic Distance Scale

No single method will provide distances on all cosmic scales. Instead, we have to rely on a multi-step approach that is carefully calibrated at each step.

This makes the Cosmic Distance Scale look like a ladder with a series of steps going from near to far:

Calibrate Parallaxes using the Astronomical Unit (orbit of the Earth)
Calibrate H-R diagram methods using stars with measured Parallaxes.
Calibrate Cepheid and RR Lyrae star distances using H-R diagrams.

Inaccuracy and imprecision at each step carries forward into the next, making each subsequent step less accurate.

Part of the challenge is to understand the sources of these inaccuracies and taking them into account.