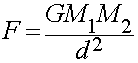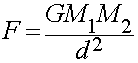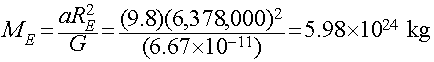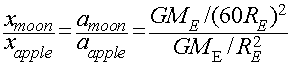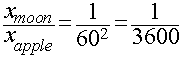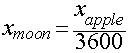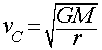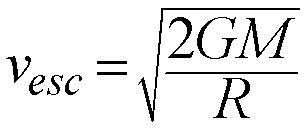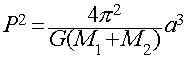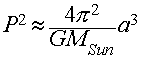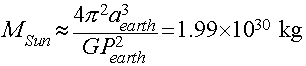Astronomy 1101: Planets to Cosmos

Gravity and Orbits

Key Ideas:

Law of Falling Bodies (Galileo)

All falling bodies experience the same gravitational acceleration

Law of Universal Gravitation (Newton)

Gravity is an attractive force between all pairs of massive objects
Gravitational force is proportional to the masses, and inversely proportional to the square of the distance between them.

Newton generalized Kepler's laws to apply to any two bodies orbiting each other

First Law: Orbits are conic sections with the center-of-mass of the two bodies at the focus.
Second Law: angular momentum conservation.
Generalized Third Law that depends on the masses of the two bodies.

Orbital Speed determines the orbit shape:

Circular Speed
Escape Speed

NOTE:
This and the following lecture are probably the most mathematical of all the lectures that will be given in this class. I encourage you all to read these notes in advance and try to follow the arguments in them. In will make it easier to follow along during lecture. [rwp]

The Law of Falling Bodies

Prior to his telescopic work, Galileo performed fundamental research on motion.

Explored the rate of falling bodies by dropping different weights, or sliding them down inclined planes.

Law of Falling Bodies

In the absence of air, heavy objects and light objects fall at the same, constant rate of acceleration.

Universal Mutual Gravitation

Isaac Newton, in his Principia, formulated the Law of Universal Mutual Gravitation:

It draws massive objects closer together
Gravity is a Universal force:: It operates everywhere in the Universe.
Gravity is a Mutual force:: It works between pairs of massive objects.

Gravitational Force

The Force of Gravity between any two objects depends only upon:

The masses of the two objects:

More massive objects exert a stronger the gravitational force.

The distance between them:

The force gets stronger as the two objects move closer together.
The force gets weaker as the two objects move farther apart.

It does not depend on the shapes, colors, or compositions of the objects.

The Law of Universal Gravitation

The force of gravitational attraction between any two massive bodies is proportional to their masses and inversely proportional to the square of the distance between their centers.

The Force of Gravity is an example of an Inverse Square Law Force

Stated mathematically, the force of gravity between two massive bodies is:

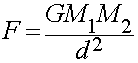
Where:: F = force due to gravity.; M₁ = mass of the first body; M₂ = mass of the second body; d = distance between their centers.; G = Gravitational Force Constant

The Gravitational Force Constant

The force constant, G, is a number which gives the size of the gravitational coupling between two massive objects.

G is very small, in metric units:

G=6.7x10^-11 Newtons meter² / kilogram²

The Newton is the metric unit of force:

4.41 Newtons = 1 pound

G has to be measured experimentally. [NOTE: G is the "gravitational coupling constant", which sets the size of the force between two massive objects separated by a given distance. Because gravity is the weakest of the 4 fundamental forces of nature, G is hard to measure experimentally with any precision. Newton did not know the value of G, but he was able to pose his problems in ways that G drops out mathematically, thus to him it was just a constant of proportionality. The first experimental measurment of G was done by British physicist Henry Cavendish in experiments performed between 1797 and 1798, using a torsion balance to measure the force of gravity between two weights in the laboratory. However, Cavendish's explicit goal for this experiment was to accurately measure the density - and hence the Mass - of the Earth, and he never once mentions G in his work or explicitly derives a value for it. Like Newton, Cavendish posed his problems so that G canceled mathematically. We'll do much the same in this class, which is why you'll never need to know G operationally for exams or homework problems. It was not until much later (almost 75 years later) that his experimental data was used by others to derive a value for G. It was not until the later part of the 19th century that astronomers needed to know G so they could, among other things, compute the densities of celestial bodies like the Moon and Sun.]

The Fall of an Apple.

Stand on the Earth and drop an apple.

What is the force of the Earth on the apple?

F = GM_earth M_apple/R_earth²

What is the apple's acceleration (Newton's 2nd Law of Motion):

a_apple = F/M_apple = GM_earth/R_earth² = 9.8 meters/sec²

Note that the mass of the apple (M_apple) had divided out of the equation. This means that the acceleration due to gravity is independent of the mass of the apple, just like Galileo had shown earlier.

Equal and Opposite Reactions

But, Newton's Third Law of Motion states that all forces come in equal yet opposite pairs

What force does the the apple apply in return upon the Earth?

F = GM_earth M_apple/R_earth²

How much does the Earth accelerate towards the apple?

a_earth = F/M_earth = GM_apple/R_earth²

This can be rewritten to give the acceleration of the Earth in terms of the acceleration of the apple towards the Earth as

a_earth = a_apple x (M_apple/M_earth)

where a_apple=9.8 meters/sec², and the ratio of the Mass of the apple to the Mass of the Earth is very small number. For a typical 200g apple, this works out to be about 10^-25 meters/sec², a very tiny acceleration.

The Mass of the Earth

We can directly measure the acceleration of gravity at the surface of the Earth by dropping objects and timing their fall (e.g., like was done by Galileo). We find

a = 9.8 meters/sec²

We can also measure the radius of the Earth using geometry (Eratosthenes):

R_earth=6378 kilometers = 6,378,000 meters

Combining these together using Newton's formula for the Gravitational Force allows us to estimate the mass of the Earth, as follows:

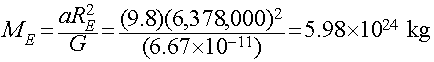
This is an example of one of the powerful implications of Newton's Law of Gravity: It gives us a way to use the motions of objects under the influence of their mutual gravitation to measure the masses of planets, stars, galaxies, etc.

The Orbit of the Moon

Falling apples are one thing, but what about the Moon?

What keeps the Moon in orbit around the Earth?

The Law of Inertia (Newton's First Law of Motion) predicts:

If there were no gravitational force acting between the Moon and the Earth, the Moon would travel in a straight line at a constant speed.

But, of course the Moon really moves along a curved path:

It is deflected from a straight-line path by the force of gravity.

This causes the Moon to fall a little bit towards the Earth at the same time at it moves to one side.

The Fall of the Moon

How far does the Moon fall around the Earth in 1 second?

Newton computed this. In order to stay in its orbit, the Moon must fall by 0.00136 meters (about 1.4 mm) each second.
Call this quantity x_moon, the deflection of the orbiting Moon in 1 second.

How far does an apple fall on the Earth during the first second?

Newton also knew this (he could measure it directly), it falls 4.9 meters in the first 1 second.
Call this quantity x_apple, the deflection of a falling apple in its 1 second of motion.

Newton also knew that:

Moon is about 60 Earth Radii from the Earth.

Summarizing the numbers:

The Moon:

Distance that the Moon falls towards Earth in 1 second: x_moon = 0.00136 meters
The distance of the Moon from the center of the Earth: d_moon = 60 R_earth
Acceleration of the Moon: a_moon = GM_earth/d_moon² = GM_earth / (60R_earth)²

The Apple:

Distance the an Apple falls on Earth in 1 second: x_apple = 4.9 meters
The distance of the Apple from the center of the Earth: d_apple = 1 R_earth
Acceleration of the Apple: a_apple = GM_earth/d_apple² = GM_earth/R_earth²

The ratio of the deflections of the Apple and the Moon in 1 second is ratio of their accelerations:

Putting all the info we have together, we get the following:

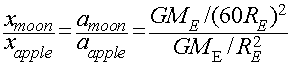
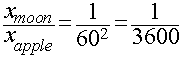
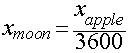
This predicts that the deflection of the Moon in 1 second necessary to keep it in orbit around the Earth should be 1/3600^th the deflection of an apple during the first second of its fall to the Earth.

Observations vs. Prediction

Is this right?

Previously we found from observations that the deflections of the Moon and apple in 1 second are:

x_moon = 0.00136 meters
x_apple = 4.9 meters

Gravity predicts that

x_apple/3600 = 4.9 meters/3600 = 0.00136 meters!!

The agreement is essentially perfect!

This demonstrates that the same law of gravity applies to both the apple and the Moon! Both feel the gravity of the Earth in the form of a force that gets weaker as the square of their distance from the center of the Earth.

So why does the Moon orbit the Earth?

If the Moon is falling a little towards the Earth, just like an apple dropped on the surface, why does the Moon travel around the Earth in an orbit instead of falling onto it?

The way to answer this question is to first consider what would happen if there was no gravity acting:

Question:: How far would the Moon travel in a straight line in 1 second if there were no gravity acting?
Answer:: About 1000 meters.

At the same time, the Moon's motion along this straight-line path would also cause it to move away from the Earth.

Question:: How far away from the Earth would the Moon move in 1 second if no gravity were acting?
Answer:: About 0.00136 meters!

In round numbers, the amount the Moon falls towards the Earth due to gravity is just enough to offset the straight-line path it would take if gravity were not acting to deflect it. This balance effectively closes the loop.

We have therefore reached a startling conclusion:

The Moon is really perpetually falling around the Earth!

This is a totally different way of looking at an "orbit" under the influence of gravity.

While at first sight the fall of an apple and the orbit of the Moon appear to be two completely different phenomena, viewed in light of Newton's laws of motion, they are in fact different manifestations of the same thing! The fall of the Moon around the Earth is the same kind of motion as the fall of an apple to the Earth. Both are described by the same three laws of motion, and both feel a gravitational force described by the same, universal force law.

Universal Gravitation

The Law of Gravity is Universal:

Governs the fall of an apple on the Earth.
Governs the fall of the Moon around the Earth.
Governs the fall of the Earth/Moon system around the Sun.
Governs the fall of the Sun around the center of the Milky Way Galaxy.
Governs the fall of the Milky Way and Andromeda Galaxies in their mutual orbit...

and so on throughout the Universe.

Kepler's Laws Revisited

Kepler's Laws of Planetary Motion are as follows:

First Law:: Planets orbit on ellipses with the Sun at one focus.
Second Law:: Planet sweeps out equal areas in equal times.
Third Law:: Period squared is proportional to the size of the semi-major axis cubed.; Expressed Mathematically as: P²=a³, for P in years and a in AUs.

Newton's Generalization

Newton showed that Kepler's Laws can be derived from

The Three Laws of Motion
The Law of Universal Gravitation.

Further, Newton generalized the laws to apply to any two bodies moving under the influence of their mutual gravitation. For example, these laws apply equally to

The Moon orbiting the Earth.
A space probe orbiting the Moon.
Two stars orbiting each other.

and so on...

First Law of Orbital Motion

The shape of an orbit is a conic section with the center of mass at one focus.

There are two parts to Newton's formulation of Kepler's First Law:

Shapes of Orbits are Conic Sections:

Curves found by cutting a cone with a plane.
Circles, Ellipses, Parabolas, and Hyperbolas

The Center of Mass is at the Focus:

Strictly speaking, it is not just the Earth orbitting the Sun. The Earth and Sun orbit each other about their mutual Center of Mass.

Because the Earth is so much smaller than the Sun, their mutual center of mass is inside the Sun, so the difference is not immediately apparent.

Conic Section Curves

These are curves formed by the intersection of a cone and a plane cutting it at various angles.

Conic curves come in two families:

Closed Curves:

Ellipses
Circles, which are a special case of an ellipse with e=0
These orbits are bound: objects will orbit forever around the parent body.

Open Curves:

Hyperbolas
Parabolas, which are a special case of a hyperbola
These orbits are unbound: objects will pass by the parent body only once and then escape from the parent body's gravity.

Which of these orbits you will be in is determined by your orbital speed. There are two special speeds of particular interest...

Circular Speed

Speed needed to sustain a circular orbit at a given radius, r, around a massive body, M:

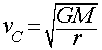
If your speed is less than v_C at your current distance, your orbit will be an ellipse smaller than the circular orbit.
If your speed is a little greater than v_C at your current distance, your orbit will be an ellipse larger than the circular orbit,
At some point, however, your speed can become large enough that you break free and escape...

This formula is only strictly valid in the case that the orbiting object is much less massive than the central massive body. For example, it is correct for a satellite or astronaut, but not for the Moon.

Escape Speed

This is the minimum speed required to escape the gravity of a body of mass M starting at a distance, r, away from it:

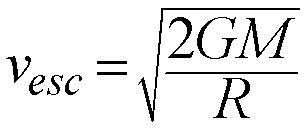
Like with circular speed, this formula is only strictly valid in the case that the moving object is much less massive than the central massive body it is "escaping from". Also, strictly speaking an object never reall "escapes" or "breaks free" from another object's gravity, it just becomes unbound and is on a trajectory that will never turn back on the bigger object like a closed or "bound" orbit.

At the Earth's surface:

v_C = 7.9 km/sec (28,400 km/hr)
v_E = 11.2 km/sec (40,300 km/hr)

Orbit Families

With these two speeds (circular and escape), we can see how the various types of closed and open conic-section orbits around a large central massive body come into being. All of the orbits shown below start from a common point, P, marked on the right (where all 5 curves intersect), but with different speeds:

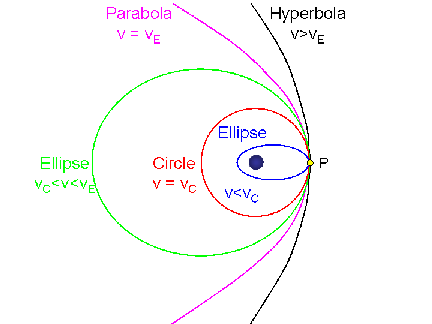
[Click on the image to view a full-size version (9k GIF)] (Graphic by R. Pogge)

Which orbit the object has is determined by the orbital speed at that point relative to the circular and escape speed at that point:

If the orbital speed is exactly the circular speed at P (V_C), the orbit will be a Circle passing through P, with the center on the central body (red curve).
If the orbital speed is slower than V_C at P, the orbit will be an Ellipse smaller than the circle that passes through P, with the central body at the far focus (blue curve).
If the orbital speed is faster than V_C at P, but less than the escape speed at P (V_E), then the orbit will be an Ellipse larger than the circular orbit that passes through P, with the central body at the near focus (green curve).
If the orbital speed is exactly the escape speed at P (V_E), the orbit will be an open Parabola (magenta curve).
If the orbital speed is greater than the escape speed from P, the orbit will be a Hyperbola (black curve). The greater the speed, the "flatter" (more open) the hyperbolic orbit.

Center of Mass

Two objects orbit about their center of mass:

Balance point between the two masses

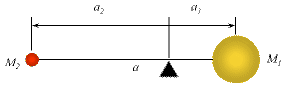
[Click on the image to view a full-size version (5Kb)](Graphic by R. Pogge)

Semi-Major axis: a = a₁ + a₂
Relative positions: a₂/ a₁ = M₁/ M₂

Example: Earth and Sun

M_sun = 2 x 10³⁰ kg

M_earth = 6 x 10²⁴ kg

From the balance relation, the distances of the Sun and Earth from their mutual center of mass are related to the size of the semi-major axis of the Earth's orbit (a) and the ratio of the masses:

a_sun + a_earth = 1 AU = 1.5 x 10⁸ km

a_sun/a_earth = M_earth/M_sun = 3 x 10^-6

After some simple algebra (do it!), we find:

a_sun = 450 km

Since the radius of the Sun is 700,000 km, this means that the center-of-mass of the Earth-Sun system is deep inside the Sun.

Second Law of Orbital Motion

Orbital motions conserve angular momentum.

This doesn't sound much like "equal areas in equal times", but in fact it is the same thing.

Angular Momentum:

L = mvr = constant
Where:: m = mass,; v = speed,; r = distance from the center of mass.

This formula is a simplification for the case of a circular orbit, but it illustrates the basic effect. In general, the angular momentum is a vector, equal to the mass times the vector cross-product of the radial vector and the velocity vector in 3 dimensions.

Angular Momentum & Equal Areas

Angular Momentum is conserved, which means that L is a constant.

If the distance changes, the speed must change to compensate so as to keep L constant:

Near Perihelion:

Planet is closer to the Sun, so r is smaller.
The speed v must be proportionally faster to compensate.

Near Aphelion:

Planet is farther to the Sun, so r is larger.
The speed v must be proportionally slower to compensate.

A familiar example of the same principle at work is a figure skater doing a spin. In an "upright spin", the skater stands on one leg with arms outstretched and spins about an up/down axis. The spin is accelerated by the skater drawing in his/her arms. By drawing in his/her arms, they are moving mass closer to the center of their body, and conservation of angular momentum demands that they spin faster.

Third Law of Orbital Motion

Newton's Generalization of Kepler's 3^rd Law:

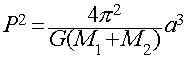
Where:: P = period of the orbit; a = semi-major axis of the orbit; M₁ = mass of the first body; M₂ = mass of the second body

A Third Law for Every Body

The proportionality between the square of the period and the cube of the semi-major axis now depends on the masses of the two bodies.

For planets orbiting the Sun, M_sun is so much bigger than any planet (even Jupiter, at 1/1000^th M_sun), that we recover Kepler's version of the Third Law from Newton's more general form:

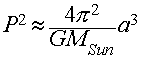
Note that the constant of proportionality is the same for all planets (to a good approximation, certainly to within Kepler's data from Tycho).

In Kepler's version, the constant of proportionality works out to be 1.0 if we use units of years for P and AUs for the semi-major axis, a. While computationally convenient, it hides the underlying dependence on the mass of the Sun from sight. The problem with empirical laws, like Kepler's formulation, is that they only show the surface, not the important details underlying them.

Measuring Masses

Newton's generalized form of Kepler's 3rd law gives us a way to measure masses from orbital motions!

For exampl, we can derive the mass of the Sun by using the period and size of the Earth's orbit:

P_earth = 1 year = 3.156 x 10⁷ seconds

a_earth = 1 AU = 1.496 x 10¹¹ meters

Using Newton's Form of Kepler's 3rd law for the solar system above, we see that once we know P and a (G and pi are constants), the only unknown is the Mass of the Sun, which can be solved for easily after a little light algebra:

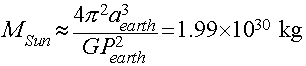
(You can verify the numbers for yourself by using G=6.67 x 10^-11 Newton m²/kg², and the values of P and a for the Earth given above in seconds and meters. Do it!).

A Universal Method for Measuring Masses

The generalized form of Kepler's Third law gives us a powerful tool for measuring the masses of objects by measuring the periods and sizes of their orbits. For example:

We can measure the mass of Jupiter from the orbits of the Galilean moons, since M_Jupiter>>M_moons

Find M_Jupiter = 300 M_earth

We can measure the total mass of the Earth and Moon system.

Earth is only ~81x more massive than the Moon, so you have to use the full formula.
Get the mass of the Earth independently (e.g., our falling bodies experiment from yesterday's lecture).

We can measure the masses of binary stars using the full formula and by observing their orbit parameters (you will see this done in Astronomy 162).

The Why of Planetary Motions

Kepler's Laws are descriptions of the motion:

Arrived at by trial and error, and some vague notions about celestial harmonies
Only describe the motions, without explaining why they move that way.

Newton provides the explanation:

Kepler's Laws are a natural consequence of Newton's Three Laws of Motion and his law of universal gravitation.

By addressing the why, Newton gave his laws predictive power that allows us to use them as tools to explore the Universe, both figuratively and literally. We can predict new phenomena or understand oddities in the motions (they laws give us a framework in which to interpret data), and we can literally use them to fly spacecraft through the solar system.