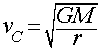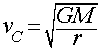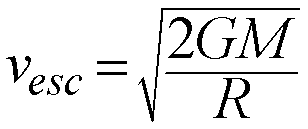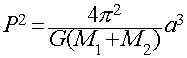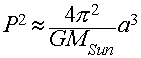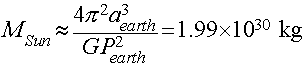Astronomy 161:
An Introduction to Solar System Astronomy
|
Lecture 19: Orbits
Key Ideas:
Newton generalized Kepler's laws to apply to any two
bodies orbiting each other
- First Law: Orbits are conic sections with the center-of-mass
of the two bodies at the focus.
- Second Law: angular momentum conservation.
- Generalized Third Law that depends on the masses of the two bodies.
Orbital Speed determines the orbit shape:
- Circular Speed
- Escape Speed
Kepler's Laws Revisited
Kepler's Laws of Planetary Motion are as follows:
- First Law:
- Planets orbit on ellipses with the Sun at one focus.
- Second Law:
- Planet sweeps out equal areas in equal times.
- Third Law:
- Period squared is proportional to the size of the
semi-major axis cubed.
- Expressed Mathematically as: P2=a3,
for P in years and a in AUs.
Newton's Generalization
Newton showed that Kepler's Laws can be derived from
- The Three Laws of Motion
- The Law of Universal Gravitation.
Further, Newton generalized the laws to apply to any
two bodies moving under the influence of their mutual gravitation. For
example, these laws apply equally to
- The Moon orbiting the Earth.
- A space probe orbiting the Moon.
- Two stars orbiting each other.
and so on...
- The shape of an orbit is a conic section with the
center of mass at one focus.
There are two parts to Newton's formulation of Kepler's First Law:
Shapes of Orbits are Conic Sections:
- Curves found by cutting a cone with a plane.
- Circles, Ellipses, Parabolas, and Hyperbolas
The Center of Mass is at the Focus:
- Strictly speaking, it is not just the Earth orbitting the Sun.
The Earth and Sun orbit each other about their
mutual Center of Mass.
Because the Earth is so much smaller than the Sun, their mutual center
of mass is inside the Sun, so the difference is not immediately apparent.
Conic Section Curves
These are curves formed by the intersection of a cone and a plane
cutting it at various angles.
Conic curves come in two families:
Closed Curves:
- Ellipses
- Circles, which are a special case of an ellipse with e=0
- These orbits are bound: objects will orbit forever
around the parent body.
Open Curves:
- Hyperbolas
- Parabolas, which are a special case of a hyperbola
- These orbits are unbound: objects will pass by the parent body
only once and then escape from the parent body's gravity.
Which of these orbits you will be in is determined by your orbital
speed. There are two special speeds of particular interest...
Speed needed to sustain a circular orbit at a given radius, r, around
a massive body, M:
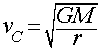
- If your speed is less than vC at your current distance,
your orbit will be an ellipse smaller than the circular orbit.
- If your speed is a little greater than vC at your current
distance, your orbit will be an ellipse larger than the circular
orbit,
- At some point, however, your speed can become large enough that you
break free and escape...
This formula is only strictly valid in the case that the orbiting object is much less massive than the central massive body. For example, it is correct for a satellite or astronaut, but not for the Moon.
This is the minimum speed required to escape the gravity of a body of
mass M starting at a distance, r, away from it:
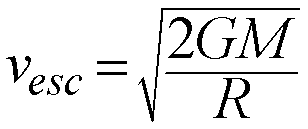
Like with circular speed, this formula is only strictly valid in the case that the moving object is much less massive than the central massive body it is "escaping from". Also, strictly speaking an object never reall "escapes" or "breaks free" from another object's gravity, it just becomes unbound and is on a trajectory that will never turn back on the bigger object like a closed or "bound" orbit.
At the Earth's surface:
- vC = 7.9 km/sec (28,400 km/hr)
- vE = 11.2 km/sec (40,300 km/hr)
Orbit Families
With these two speeds (circular and escape), we can see how the various
types of closed and open conic-section orbits around a large central
massive body come into being. All of the orbits shown below start from
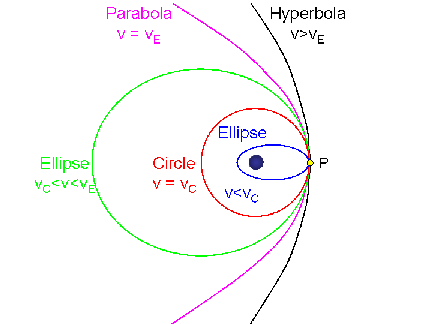
a common point, P, marked on the right (where all 5 curves intersect),
but with different speeds:
- [Click on the image to view a full-size version (9k GIF)]
(Graphic by R. Pogge)
Which orbit the object has is determined by the orbital speed at
that point relative to the circular and escape speed at that point:
- If the orbital speed is exactly the circular speed at P (VC), the orbit will be a Circle
passing through P, with the center on the central body (red curve).
- If the orbital speed is slower than VC at P, the
orbit will be an Ellipse smaller than the circle that passes through
P, with the central body at the far focus (blue curve).
- If the orbital speed is faster than VC at P, but
less than the escape speed at P (VE), then the orbit will be an Ellipse
larger than the circular orbit that passes through P, with the
central body at the near focus (green curve).
- If the orbital speed is exactly the escape speed at P (VE), the orbit will be an open
Parabola (magenta curve).
- If the orbital speed is greater than the escape speed from P,
the orbit will be a Hyperbola (black curve). The greater the
speed, the "flatter" (more open) the hyperbolic orbit.
Center of Mass
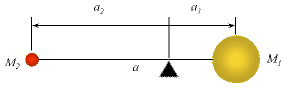
Two objects orbit about their center of mass:
- Balance point between the two masses
[Click on the image to view a full-size version (5Kb)](Graphic by R. Pogge)
- Semi-Major axis: a = a1 + a2
- Relative positions: a2 / a1
= M1 / M2
Example: Earth and Sun
- Msun = 2 x 1030 kg
- Mearth = 6 x 1024 kg
From the balance relation, the distances of the Sun and Earth from
their mutual center of mass are related to the size of the semi-major
axis of the Earth's orbit (a) and the ratio of the masses:
- asun + aearth = 1 AU = 1.5 x 108 km
- asun/aearth = Mearth/Msun
= 3 x 10-6
After some simple algebra (do it!), we find:
- asun = 450 km
Since the radius of the Sun is 700,000 km, this means that the
center-of-mass of the Earth-Sun system is deep inside the
Sun.
- Orbital motions conserve angular momentum.
This doesn't sound much like "equal areas in equal times",
but in fact it is the same thing.
Angular Momentum:
- L = mvr = constant
- Where:
- m = mass,
- v = speed,
- r = distance from the center of mass.
This formula is a simplification for the case of a circular orbit, but it illustrates the basic effect. In general, the angular momentum is a vector, equal to the mass times the vector cross-product of the radial vector and the velocity vector in 3 dimensions.
Angular Momentum & Equal Areas
Angular Momentum is conserved, which means that L is a
constant.
If the distance changes, the speed must change to
compensate so as to keep L constant:
Near Perihelion:
- Planet is closer to the Sun, so r is smaller.
- The speed v must be proportionally faster to compensate.
Near Aphelion:
- Planet is farther to the Sun, so r is larger.
- The speed v must be proportionally slower to compensate.
A familiar example of the same principle at work is a figure skater
doing a spin. In an "upright spin", the skater stands on one leg with
arms outstretched and spins about an up/down axis. The spin is
accelerated by the skater drawing in his/her arms. By drawing in
his/her arms, they are moving mass closer to the center of their body,
and conservation of angular momentum demands that they spin faster.
Newton's Generalization of Kepler's 3rd
Law:
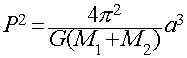
- Where:
- P = period of the orbit
- a = semi-major axis of the orbit
- M1 = mass of the first body
- M2 = mass of the second body
A Third Law for Every Body
The proportionality between the square of the period and the
cube of the semi-major axis now depends on the masses of
the two bodies.
For planets orbiting the Sun, Msun is so much bigger than any
planet (even Jupiter, at 1/1000th Msun), that we
recover Kepler's version of the Third Law from Newton's more general
form:
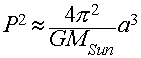
Note that the constant of proportionality is the same for all planets
(to a good approximation, certainly to within Kepler's data from Tycho).
In Kepler's version, the constant of proportionality works out to be 1.0
if we use units of years for P and AUs for the semi-major axis, a. While
computationally convenient, it hides the underlying dependence on the mass
of the Sun from sight. The problem with empirical laws, like Kepler's
formulation, is that they only show the surface, not the important details
underlying them.
Measuring Masses
Newton's generalized form of Kepler's 3rd law gives
us a way to measure masses from orbital motions!
For exampl, we can derive the mass of the Sun by using the
period and size of the Earth's orbit:
- Pearth = 1 year = 3.156 x 107 seconds
- aearth = 1 AU = 1.496 x 1011 meters
Using Newton's Form of Kepler's 3rd law for the solar system
above, we see that once we know P and a (G and pi are constants),
the only unknown is the Mass of the Sun, which can be solved for
easily after a little light algebra:
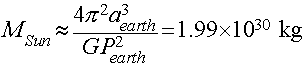
(You can verify the numbers for yourself by using G=6.67 x
10-11 Newton m2/kg2, and the values of
P and a for the Earth given above in seconds and meters. Do it!).
A Universal Method for Measuring Masses
The generalized form of Kepler's Third law gives us a powerful
tool for measuring the masses of objects by measuring the periods
and sizes of their orbits. For example:
We can measure the mass of Jupiter from the orbits of the
Galilean moons, since MJupiter>>Mmoons
- Find MJupiter = 300 Mearth
We can measure the total mass of the Earth and Moon system.
- Earth is only ~81x more massive than the Moon, so you
have to use the full formula.
- Get the mass of the Earth independently (e.g., our
falling bodies experiment from yesterday's lecture).
We can measure the masses of binary stars using the full
formula and by observing their orbit parameters (you will see
this done in Astronomy 162).
The Why of Planetary Motions
Kepler's Laws are descriptions of the motion:
- Arrived at by trial and error, and some vague notions
about celestial harmonies
- Only describe the motions, without explaining why they
move that way.
Newton provides the explanation:
- Kepler's Laws are a natural consequence of Newton's Three Laws of
Motion and his law of universal gravitation.
By addressing the why, Newton gave his laws predictive power that allows
us to use them as tools to explore the Universe, both figuratively and
literally. We can predict new phenomena or understand oddities in the
motions (they laws give us a framework in which to interpret data), and
we can literally use them to fly spacecraft through the solar system.
Updated: 2010 October 10, Todd A. Thompson
Copyright © Richard W. Pogge,
All Rights Reserved.