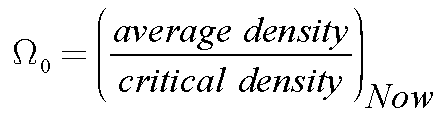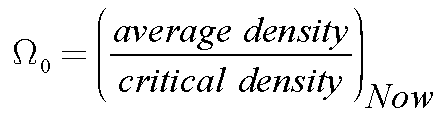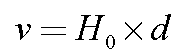Astronomy 162: Introduction to Stars, Galaxies, and Cosmology

Todd Thompson
Department of Astronomy
The Ohio State University

Lecture 35: The Big Bang

Key Ideas

Big Bang Model of the Universe: The Universe started in a hot, dense state; Universe expands and cools with time
Cosmological Redshift & Lookback Time
Critical Density: Determines the Geometry of the Universe; Influences the expansion history of the Universe
Hubble Time: Estimate of the Age of the Universe

Expansion of the Universe

The Universe is observed to be expanding today.

Evidence: Hubble's Law

As the Universe expands, it cools.

In the past, it must therefore have been:

smaller
denser
hotter

than it is today.

The Big Bang

If we run the clock backwards far enough, eventually the Universe would be

very small & very high density
Very very hot & opaque

This initial state must have existed at some finite time in the past.

We call this very hot, very dense initial state "The Big Bang"

Foundations of the Big Bang

An infinitely dense and hot Universe in the past follows naturatlly from three basic physical assumptions:

General Relativity is valid on cosmic scales.
The Universe is homogeneous and isotropic on cosmic scales.
The energy of the vacuum is either zero or very small (the Cosmological Constant: L)

All of these assumptions are testable observationally.

The Big Bang is a Testable Model

These basic assumptions are plausible:

Supported by empirical data for the most part
Have Reasonably sound physical basis

But, they are not required to be true.

The Real Test:

Does the Big Bang Model explain the properties of the observed Universe?

It is important to emphasize that this is why we think this is an important idea. The Big Bang is not just a conjecture: it makes powerful predictions that can be tested against observations. If it could not be tested, it would have no use to us as a model for the evolution of the Universe.

Expansion & Hubble's Law

As the Universe expands:

Space gets stretched in all directions.
Matter is carried along with the expanding space.
The distances between galaxies get larger with time.

The Big Bang predicts Hubble's Law exactly for recession speeds that are small compared to the speed of light.

Note that a more detailed description is required at large cosmological distances that takes into account the detailed geometry of the Universe.

Cosmological Redshift

The expansion of space also stretches light waves:

Wavelengths get stretched into longer and hence redder wavelengths.
The greater the distance, the greater the stretching.

Result:

The redshift of an object gets larger with increasing distance.

The Big Bang naturally explains the observed Cosmological Redshift, distinguishing it from a normal Doppler Shift due to objects moving through space rather than expanding with space.

Cosmic Lookback Time

We observe the Universe using light, but light moves at a finite speed:

It takes time for light to reach you from a distant source.
Example: we see the Sun as it was ~8.5 minutes ago due to the time it takes light to travel 1AU.

At cosmic distances, the effect is even more pronounced:

The deeper we look into the Universe, the further we are actually looking back in cosmic time to when the Universe was younger and smaller.

This fact allows us to reconstruct the past expansion history of the Universe, provided, as always, that we can measure distances accurately.

This is a startling fact: cosmic lookback time means that we can actually observe the Big Bang unfolding from the past to the present!

The Shape of the Universe

All forms of matter attract each other via their mutual gravity.

Relativity tells us that:

Energy is equivalent to mass (E=mc²), so all forms of energy in the Universe gravitate as well.
Matter & energy combined tell spacetime how to curve.

The combined matter and energy density of the Universe determines its global geometry.

The Density Parameter, W₀

The geometry of the Universe depends on the total density of matter and energy:

High Density

Positively curved (spherical) geometry

Low Density

Negatively curved (hyperbolic) geometry

Dividing Line: Critical Density

Universe is Flat: no curvature

We express this in terms of a Density Parameter, W₀:

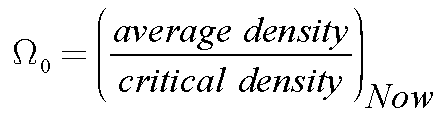
(Graphic by R. Pogge)

The Density Parameter is the ratio of the current density of matter and energy in the Universe to the "Critical Density" needed for a spatially-flat Universe.

The Geometry of the Universe

The important values of W₀ are as follows:

W₀ > 1: positive curvature

Finite yet unbounded spherical Universe
Parallel light rays converge
W₀ < 1: negative curvature

Infinite, hyperbolic Universe
Parallel light rays diverge
W₀ = 1: Critical (Flat) Universe

Infinite, flat Universe
Parallel light rays stay parallel

Back to the Beginning

The Universe is expanding now.

In the past:

Universe was smaller.
Galaxies were closer together in space.

If we go back far enough in time:

All galaxies (matter) in one place.

How far back = "Age of the Universe"

Road Trip Analogy

You leave Columbus by car for Florida, but leave your watch behind.

How long have you been on the road?

Your average speed = 100 km/h
Your odometer reads: distance = 230 km

Time since you left: T = distance / speed

T = 230 km / 100 km/h = 2.30 hours

The Hubble Time, T₀

Hubble's Law says

A galaxy at distance d away has a recession speed, v, given by the Hubble Law:

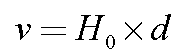
Graphic by R. Pogge)

If locally, v is about its average speed, then:

T = d / v
but since, v = H₀ d, and T = d/H₀ d = 1 / H₀

This defines the Hubble Time:

T₀ = 1 / H₀

This provides an estimate of how long the Universe has been expanding, and hence its age.

But...

The rate of cosmic expansion is not expected to be constant over all times:

If the expansion were faster in the past:

Expansion would be slowed down by the gravity of all the matter and energy in the Universe.
T₀ would overestimate the age of the Universe.

If the expansion were slower in the past:

Expansion might be accelerated by a non-zero cosmological constant (L).
T₀ would underestimate the age of the Universe.

So, How old is it really?

We need to know the values of two hard-to-measure numbers:

Hubble Parameter, H₀:

Tells us how fast the universe is expanding now.

Density Parameter, W₀:

Tells us how the matter & energy density of the Universe affects the expansion rate.
Can include an W_L term (aka a "Cosmological Constant") that enhances the expansion rate.

These are needed to be able to determine the expansion history of the Universe.

The Age of the Universe:

Our best current estimate of the Age of the Universe is about

T₀ = 13.7 Gyr

This value is found by using the current "Benchmark" (or "Concordance") Cosmology:

H₀ = 70 +/- 7 km/sec/Mpc
W₀ = W_m + W_L=1.0

The value W₀ consists of a 30% contribution from all forms of matter (W_m=0.3), and a 70% contribution from the energy density (W_L=0.7).

This value of W₀=1 implies that we live in an infinite, spatially flat Universe.

This age is consistent with the ages of the oldest stars seen in globular clusters.