(Click on the image to view at full scale [Size: 7Kb];(Graphic by R. Pogge) )
Todd Thompson
Department of Astronomy
The Ohio State University
d=1/p
Examples of such problems:
Answer:

(Click on the image to view at full scale [Size: 7Kb];(Graphic by R. Pogge)
)
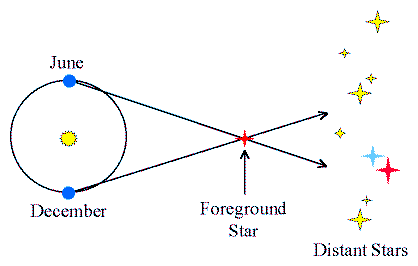
In the picture above, the line of sight to the star in December is different than that in June, when the Earth is on the other side of its orbit. As seen from the Earth, the nearby star appears to sweep through the angle shown. Half of this angle, is the parallax, p.
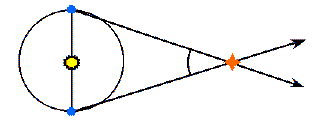

In the upper figure, the star is about 2.5 times nearer than the star in the lower figure, and has a parallax angle which is 2.5 times larger.
This movie demonstrates parallaxes graphically.
This gives us a means to measure distances directly by measuring the parallaxes of nearby stars.
We call this powerful direct distance technique the Method of Trigonometric Parallaxes.
For example, the nearest star, Proxima Centauri, has a parallax of 0.772-arcsec (the largest parallax observed for any star).
1 arcsecond (1'') is the angle subtended by a dime at a distance of 2.3 miles.
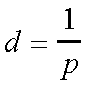
Where:
Writing our parallax formula in this way allows us to define a new "natural" unit for distances in astronomy: the Parallax-Second or Parsec.
In words: The distance of a star in parsecs is one over its parallax in arc-seconds.
1 parsec (pc) is equivalent to:
1 light year (ly) is equivalent to:
The light year is rarely used in research astronomy.
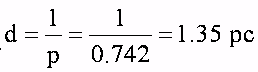
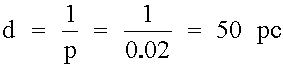
Additional information on parallax here here and here and here.
In general, the greater the distance, the smaller the parallax, and so the less precise the distance measurement will be.
The smallest parallax measurable from the ground is about 0.01-arcsec. This means that from the ground, the method of Trigonometric Parallaxes has the following limitations.

The Hipparcos satellite (launched by the European Space Agency in 1989) measured precision parallaxes to an accuracy of about 0.001-arcsec.
Hipparcos represented a great leap in our knowledge of the distances (and motions) of nearby stars. The catalog was just released in late 1997, and is already having an impact on many areas of astronomy that rely in accurate distances.
For more information about the Hipparcos mission, visit the Hipparcos Web Site at ESA Astrophysics.
SIM is a proposed NASA mission to use the emerging technique of optical interferometry to make high-precision angular measurements. A firm launch date has not been set, but it would be no sooner than 2012....
Update: SIM is cancelled. More information here
One of SIM mission's key projects is to map the Galaxy using accurate stellar parallaxes. SIM's technical goal is to achieve a parallax precision of ~4 microacseconds, which would yield 10% distances out to 25,000 parsecs, encompassing the Galatic Center (8000pc away) and the halo of the Galaxy. SIM's science projects will select particular targets througout the Galaxy to perform focussed "pointed" studies, rather than measuring every star down to some brightness limit.
SIM is an ambitious mission with many important science goals, to learn more visit the SIM webpage at NASA's Jet Propulsion Labortory.
Gaia
Gaia is a proposed European follow-up mission to Hipparcos currently slated for a late-2011 launch. It's goal is to conduct what amounts to a Galactic census. Unlike SIM, which is a pointed mission, Gaia will attempt an all-sky survey of the Galaxy that build up high-precision angular measurements through repeated measurements (whereas SIM can achieve high precision in single measurements).
Mission Goals: