Astronomy 1144: Introduction to Stars, Galaxies, and Cosmology

Todd Thompson
Department of Astronomy
The Ohio State University

Lecture 6: Stars II: Motions

Key Ideas

The stars are in constant motion.

Observed Motions:
Proper Motions (across the sky)
Radial Velocity (towards/away from us)

True Space Motion
Combination of radial velocity, proper motion, & distance.

Key Equations

Vt = 4.74 μ d

V2 = Vr2 + Vt2

The "Fixed Stars"

To the naked eye, the stars appear "fixed" to the sky. In reality, the stars are in constant motion. The great distances to the stars means that their apparent motions across the sky are very small during a human lifetime.

Proper Motions

Proper Motion is the apparent angular motion of a star across the sky with respect to more distant stars.

This is the projection onto the sky of the star's true motions through space relative to the Sun.

Proper motions are Cumulative.

The effect of proper motions build up over time...

Modern measurement of proper motions:

Example:

Consider a star with a proper motion of 0.1 arcsec/year:

Since the smallest angle the eye can discern with great care is a few arcminutes (1 arcmin = 60 arcsec), it can take many millennia for the constellations to noticeably change shape.

Discovery

Proper motions were first noted by Edmund Halley in 1718 for three bright stars: Sirius, Aldebaran, and Arcturus, by comparing his measurements of their positions to those of Hipparchus of Rhodes (300BC). In all, it took 2000 years for the motions to build up to the point that they became apparent to naked eye observers.

Case Study: Proper motions in the Big Dipper

Due to the proper motions of the stars that make up this familiar constellation, its shape changes slowly over time. It takes many thousands of years, however, for the effects to be visible to the naked eye.

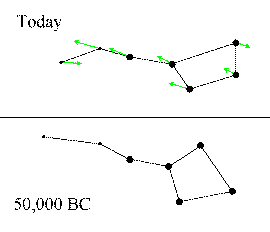
50,000 years of proper motions in UMa

(Graphic by R. Pogge)

Here is a movie showing 200,000 years of proper motion in the Big Dipper, including faint stars. Notice how they all tend to move in different directions, but some (like 5 in the Dipper) have common motions...

Proper Motion depends on the Distance

The amount of proper motion shown by a star depends on its distance.

Distance Effect in Proper Motions

(Graphic by R. Pogge)

But...

Distance is only part of the effect!

A small proper motion does not always mean a large distance!

Example:

Stars moving exactly towards or away from us will show no proper motions!

No P.M. in pure radial motion

(Graphic by R. Pogge)

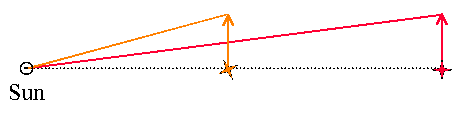
Radial Velocity

The radial velocity of a star is how fast it is moving directly towards or away from us.

Radial Motions

(Graphic by R. Pogge)

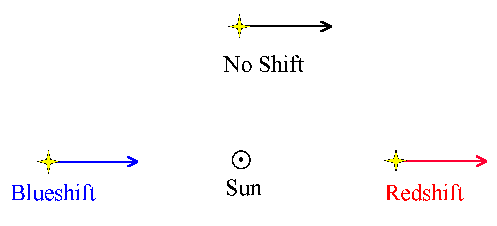
Radial velocities are measured using the Doppler Shift of the star's spectrum:

In all cases, the Radial Velocity is Independent of Distance.

True Space Motions

The quantity we really want to know is the true motion of the star through space in 3-dimensions.

To find the true space velocity of a star, we need to break its motions into two velocity components:

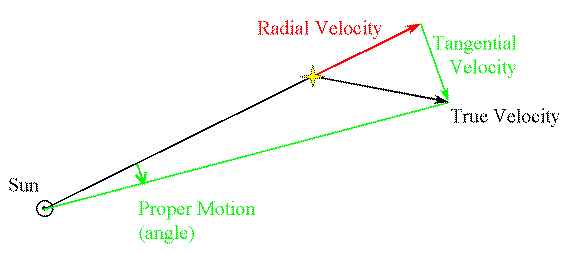
decomposition of true motion into radial and tangential parts

(Graphic by R. Pogge)

Radial Velocity (vr)
Measure this using the Doppler Shift of its spectrum.

Tangential Velocity (vt)
Measure this from its Proper Motion and Distance:

Vt = 4.74 μ d

where:
μ = Proper Motion in arcsec/yr
d = Distance in parsecs

The formula above gives vt in km/sec.

Each of these velocities forms the legs of a right triangle with the true space velocity (v) as the hypotenuse.

We can then use the Pythagorean Theorem to derive the True Space Velocity (v):

V2 = Vr2 + Vt2

V2 = Vr2 + (4.74 μ d)2

To estimate the true space velocity, you need to measure three observable quantities:

The last is often the most difficult to measure (as always).

Why measure the space motions?

Most useful when measured for many stars.

Use statistics of the motions to find:

Stellar motions are an important tool for studying the structure of our home galaxy, the Milky Way.

Updated 8/25/2013 Todd Thompson
Original Version by R. Pogge.