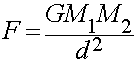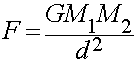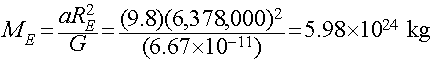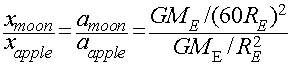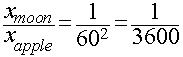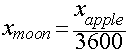Astronomy 161:
An Introduction to Solar System Astronomy

Lecture 18: The Apple and the Moon:
Newtonian Gravity

Key Ideas:

Law of Falling Bodies (Galileo)

All falling bodies experience the same gravitational acceleration

Law of Universal Gravitation (Newton)

Gravity is an attractive force between all pairs of massive objects
Gravitational force is proportional to the masses, and inversely proportional to the square of the distance between them.

NOTE:
This and the following lecture are probably the most mathematical of all the lectures that will be given in this class. I encourage you all to read these notes in advance and try to follow the arguments in them. In will make it easier to follow along during lecture. [rwp]

The Law of Falling Bodies

Prior to his telescopic work, Galileo performed fundamental research on motion.

Explored the rate of falling bodies by dropping different weights, or sliding them down inclined planes.

Law of Falling Bodies

In the absence of air, heavy objects and light objects fall at the same, constant rate of acceleration.

Universal Mutual Gravitation

Isaac Newton, in his Principia, formulated the Law of Universal Mutual Gravitation:

It draws massive objects closer together
Gravity is a Universal force:: It operates everywhere in the Universe.
Gravity is a Mutual force:: It works between pairs of massive objects.

Gravitational Force

The Force of Gravity between any two objects depends only upon:

The masses of the two objects:

More massive objects exert a stronger the gravitational force.

The distance between them:

The force gets stronger as the two objects move closer together.
The force gets weaker as the two objects move farther apart.

It does not depend on the shapes, colors, or compositions of the objects.

The Law of Universal Gravitation

The force of gravitational attraction between any two massive bodies is proportional to their masses and inversely proportional to the square of the distance between their centers.

The Force of Gravity is an example of an Inverse Square Law Force

Stated mathematically, the force of gravity between two massive bodies is:

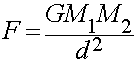
Where:: F = force due to gravity.; M₁ = mass of the first body; M₂ = mass of the second body; d = distance between their centers.; G = Gravitational Force Constant

The Gravitational Force Constant

The force constant, G, is a number which gives the size of the gravitational coupling between two massive objects.

G is very small, in metric units:

G=6.7x10^-11 Newtons meter² / kilogram²

The Newton is the metric unit of force:

4.41 Newtons = 1 pound

G has to be measured experimentally. [NOTE: G is the "gravitational coupling constant", which sets the size of the force between two massive objects separated by a given distance. Because gravity is the weakest of the 4 fundamental forces of nature, G is hard to measure experimentally with any precision. Newton did not know the value of G, but he was able to pose his problems in ways that G drops out mathematically, thus to him it was just a constant of proportionality. The first experimental measurment of G was done by British physicist Henry Cavendish in experiments performed between 1797 and 1798, using a torsion balance to measure the force of gravity between two weights in the laboratory. However, Cavendish's explicit goal for this experiment was to accurately measure the density - and hence the Mass - of the Earth, and he never once mentions G in his work or explicitly derives a value for it. Like Newton, Cavendish posed his problems so that G canceled mathematically. We'll do much the same in this class, which is why you'll never need to know G operationally for exams or homework problems. It was not until much later (almost 75 years later) that his experimental data was used by others to derive a value for G. It was not until the later part of the 19th century that astronomers needed to know G so they could, among other things, compute the densities of celestial bodies like the Moon and Sun.]

The Fall of an Apple.

Stand on the Earth and drop an apple.

What is the force of the Earth on the apple?

F = GM_earth M_apple/R_earth²

What is the apple's acceleration (Newton's 2nd Law of Motion):

a_apple = F/M_apple = GM_earth/R_earth² = 9.8 meters/sec²

Note that the mass of the apple (M_apple) had divided out of the equation. This means that the acceleration due to gravity is independent of the mass of the apple, just like Galileo had shown earlier.

Equal and Opposite Reactions

But, Newton's Third Law of Motion states that all forces come in equal yet opposite pairs

What force does the the apple apply in return upon the Earth?

F = GM_earth M_apple/R_earth²

How much does the Earth accelerate towards the apple?

a_earth = F/M_earth = GM_apple/R_earth²

This can be rewritten to give the acceleration of the Earth in terms of the acceleration of the apple towards the Earth as

a_earth = a_apple x (M_apple/M_earth)

where a_apple=9.8 meters/sec², and the ratio of the Mass of the apple to the Mass of the Earth is very small number. For a typical 200g apple, this works out to be about 10^-25 meters/sec², a very tiny acceleration.

The Mass of the Earth

We can directly measure the acceleration of gravity at the surface of the Earth by dropping objects and timing their fall (e.g., like was done by Galileo). We find

a = 9.8 meters/sec²

We can also measure the radius of the Earth using geometry (Eratosthenes):

R_earth=6378 kilometers = 6,378,000 meters

Combining these together using Newton's formula for the Gravitational Force allows us to estimate the mass of the Earth, as follows:

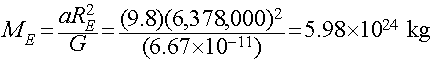
This is an example of one of the powerful implications of Newton's Law of Gravity: It gives us a way to use the motions of objects under the influence of their mutual gravitation to measure the masses of planets, stars, galaxies, etc.

The Orbit of the Moon

Falling apples are one thing, but what about the Moon?

What keeps the Moon in orbit around the Earth?

The Law of Inertia (Newton's First Law of Motion) predicts:

If there were no gravitational force acting between the Moon and the Earth, the Moon would travel in a straight line at a constant speed.

But, of course the Moon really moves along a curved path:

It is deflected from a straight-line path by the force of gravity.

This causes the Moon to fall a little bit towards the Earth at the same time at it moves to one side.

The Fall of the Moon

How far does the Moon fall around the Earth in 1 second?

Newton computed this. In order to stay in its orbit, the Moon must fall by 0.00136 meters (about 1.4 mm) each second.
Call this quantity x_moon, the deflection of the orbiting Moon in 1 second.

How far does an apple fall on the Earth during the first second?

Newton also knew this (he could measure it directly), it falls 4.9 meters in the first 1 second.
Call this quantity x_apple, the deflection of a falling apple in its 1 second of motion.

Newton also knew that:

Moon is about 60 Earth Radii from the Earth.

Summarizing the numbers:

The Moon:

Distance that the Moon falls towards Earth in 1 second: x_moon = 0.00136 meters
The distance of the Moon from the center of the Earth: d_moon = 60 R_earth
Acceleration of the Moon: a_moon = GM_earth/d_moon² = GM_earth / (60R_earth)²

The Apple:

Distance the an Apple falls on Earth in 1 second: x_apple = 4.9 meters
The distance of the Apple from the center of the Earth: d_apple = 1 R_earth
Acceleration of the Apple: a_apple = GM_earth/d_apple² = GM_earth/R_earth²

The ratio of the deflections of the Apple and the Moon in 1 second is ratio of their accelerations:

Putting all the info we have together, we get the following:

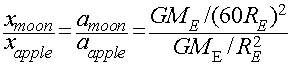
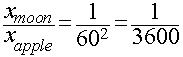
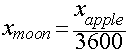
This predicts that the deflection of the Moon in 1 second necessary to keep it in orbit around the Earth should be 1/3600^th the deflection of an apple during the first second of its fall to the Earth.

Observations vs. Prediction

Is this right?

Previously we found from observations that the deflections of the Moon and apple in 1 second are:

x_moon = 0.00136 meters
x_apple = 4.9 meters

Gravity predicts that

x_apple/3600 = 4.9 meters/3600 = 0.00136 meters!!

The agreement is essentially perfect!

This demonstrates that the same law of gravity applies to both the apple and the Moon! Both feel the gravity of the Earth in the form of a force that gets weaker as the square of their distance from the center of the Earth.

So why does the Moon orbit the Earth?

If the Moon is falling a little towards the Earth, just like an apple dropped on the surface, why does the Moon travel around the Earth in an orbit instead of falling onto it?

The way to answer this question is to first consider what would happen if there was no gravity acting:

Question:: How far would the Moon travel in a straight line in 1 second if there were no gravity acting?
Answer:: About 1000 meters.

At the same time, the Moon's motion along this straight-line path would also cause it to move away from the Earth.

Question:: How far away from the Earth would the Moon move in 1 second if no gravity were acting?
Answer:: About 0.00136 meters!

In round numbers, the amount the Moon falls towards the Earth due to gravity is just enough to offset the straight-line path it would take if gravity were not acting to deflect it. This balance effectively closes the loop.

We have therefore reached a startling conclusion:

The Moon is really perpetually falling around the Earth!

This is a totally different way of looking at an "orbit" under the influence of gravity.

While at first sight the fall of an apple and the orbit of the Moon appear to be two completely different phenomena, viewed in light of Newton's laws of motion, they are in fact different manifestations of the same thing! The fall of the Moon around the Earth is the same kind of motion as the fall of an apple to the Earth. Both are described by the same three laws of motion, and both feel a gravitational force described by the same, universal force law.

Universal Gravitation

The Law of Gravity is Universal:

Governs the fall of an apple on the Earth.
Governs the fall of the Moon around the Earth.
Governs the fall of the Earth/Moon system around the Sun.
Governs the fall of the Sun around the center of the Milky Way Galaxy.
Governs the fall of the Milky Way and Andromeda Galaxies in their mutual orbit...

and so on throughout the Universe.

Lecture 18: The Apple and the Moon: Newtonian Gravity