Astronomy 161:
An Introduction to Solar System Astronomy
|
Lecture 4: Measuring the Earth
Key Ideas:
Ancient ideas about the Earth.
- Flat Earth and World Ocean
The Spherical Earth
- Appeal to perfect symmetry
- Demonstration by Aristotle
Measuring the Earth's Circumference:
- Eratosthenes of Cyrene
- Claudius Ptolemy
The Four Corners of the Earth
The most common ancient theme is that of a Flat Earth surmounted by
a hemispherical sky.
- Homeric: A flat disk surrounded by a world ocean.
- Inca: Called their land Tahuantinsuyu: "The Four
Quarters of the Earth"
- Ancient Egyptian: The sky was a tent canopy stretched
between mountains at the four corners of the Earth.
In some cultures, the canopy of the sky was held up by immense trees
or gigantic mountains.
Myth & Metaphor
These fanciful views are Representations rather than
Portrayals of reality.
- The great myths and metaphors make the world seem
intelligible and beautiful to the people who invented
them.
- They serve cultural purposes motivated by an aesthetic we
can only guess at.
Classical Greece
The Ancient Greeks were intoxicated by geometry, form, and symmetry.
A sphere is the most perfect geometric solid
- 500 BC:
- Pythagoras proposed a spherical earth purely on aesthetic
grounds
- 400 BC:
- Plato espoused a spherical earth in his 4th and final
dialogue Phaedo, giving it wider circulation
(the Pythagoreans were somewhat disreputable in Athenian circles)
Aristotle
Aristotle (384-322 BC) also proposed a spherical earth on geometric
grounds, but backed up his assertion with physical evidence
(described in his On the Heavens of 350BC. [Note:
Aristotle's arguments for the
spherical shape of the Earth are given in On the Heavens,
Book 2, Part 14 (350 BCE). A modern translation by J.L. Stokes may be
found online at MIT on the Internet
Classics Archive.
Aristotle argued that the Earth must necessarily be spherical
because the weight of all its parts setting towards the center would
naturally form a spherical shape. Today we would recognize the tendency
to settle towards the center to be a consequence of gravity (Aristotle
does not, of course, use that word).
He noted the curved outline of the shadow of the Earth on the Moon, and
the different heights of stars between orthern and southern regions, as
mentioned in the lecture, but he also put forth a rather odd argument
that one finds elephants in Africa ("Pillars of Hercules" is the Strait
of Gibraltar) and India, arguing for "continuity of parts", meaning they
are close together on the surface of a sphere (they are far apart across
the mediterranian, but closer going west from Africa). The idea being
the world conceived by Aristotle is small, but not so small that small
changes in place result in dramatic changes in the heights of constellations.]
- Persons living in southern lands see southern constellations higher
above the horizon than those living in northern lands.
- The shadow of the Earth on the Moon during a lunar eclipse is round.
- The fact that objects fall to Earth towards its center means that if
it were constructed of small bits of matter originally, these parts
would naturally settle into a spherical shape.
Aristotle's demonstration was so compelling that a spherical Earth
was the central assumption of all subsequent philosophers of the
Classical era (up to ~300 AD).
He also used the curved phases of the moon to argue that the Moon
must also be a sphere like the Earth.
How Big is the Earth?
Having established its shape, what is the size of the Earth?
Challenge: How do you measure something really big?
- Mountains too high to climb...
- The Earth too large to trail a string behind you...
Solution: Apply the methods of Geometry.
Eratosthenes of Cyrene
Born in Cyrene (now Shahhat Libya) in 276 BC. He was the 2nd Librarian
of Alexandria until his death around 195 BC.
It was known that on the day of the Summer Solstice in Syene Egypt
(modern Aswan), the Sun was straight overhead at noon and did not cast
shadows. Syene is on the lower Nile in southern Egypt.
On that same day, the noon Sun cast shadows at Alexandria, located north
of Syene on the Nile delta.
Shadowless in Syene
Eratosthenes knew that no shadows on the Summer Solstice meant that
Syene was on the boundary of the northern tropic zone (the Tropic of
Cancer).
By measuring the length of the shadow in Alexandria at noon on the
Summer Solstice when there was no shadow in Syene, he could measure the
circumference of the Earth!
High Noon on the Summer Solstice
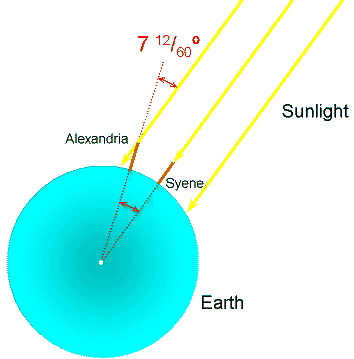
[Click on the image to view full size (34k)]
(Graphic by R. Pogge)
- At Syene:
- The Sun is directly overhead, no shadows are cast at that
moment.
- At Alexandria:
- The Sun is 712/60 degrees south of overhead,
casting shadows.
Since a full circle is 360 degrees, the arc from Alexandria to Syene is
thus approximately 1/50th of a full circle (the sun angle above
divided by 360).
Therefore, the circumference of the Earth is 50 times the distance from
Alexandria to Syene.
- Question 1: How far is Alexandria from Syene?
- 5000 stadia
- Question 2: How big is 1 stadion?
- 600 Greek Feet (length of a foot race in a Greek
"stadium")
The best modern guess is that 1 stadion = 185 meters, based on the
"Attic Stadion" measured from the Stadium at Athens.
[Note: The definition of a stadion in
modern units has been very contentious. A very compelling case has been
made by Donald Engels (1985, American Journal of Philology,
106, 298, full
article on jstor.org) for 1 stadion = 184.98 meters (based on 8 Roman
miles to 1 stadion). Two numbers reappear in the literature:
148 meters/stadion, which was a mis-calculation by d'Anville in 1759,
and 157.4 meters/stadion given by A. Letronne in 1851 (published
posthumously). I used to quote the 157m/stadion number in my notes, which
gives a circumference of the Earth much closer to that of the modern
value. Engels' arguments, however, are very persuasive that Eratosthenes
would have used the Attic Stadion based on the Stadium of Athens, which
gives the conversion of ~185m/stadion that I quote in these notes.]
Putting Eratosthenes result into modern units, his
estimate of the circumference
of the Earth is as follows:
Circumference = 50 x 5000 stadia = 250,000 stadia
250,000 stadia x 185 meters/stadion = 46,250 kilometers
The modern measurement is 40,070 kilometers.
Eratosthenes' estimate is only about 15% too large!
For more information, see the wikipedia entry for Eratosthenes
Claudius Ptolemy (c. 140 AD)
Claudius Ptolemais (Ptolemy for short) was a Geometer and Astronomer of
the late Classical Age in Alexandria. His work was immensely influential
in later centuries, as we'll see in later lectures.
Ptolemy made a similar geometric estimate based on stellar (rather than
solar) measurements made earlier by Marinus of Tyre (by way of
Posidonius). This estimate yields a circumference of 28,800 kilometers,
which is ~28% smaller than the correct circumference (40,070 km).
[Note: By Ptolemy's time, we are actually on better grounds for
converting Classical Roman units to modern units, largely because many
Roman roads and measuring techniques have survived from antiquity.]
For more information, see the wikipedia entry for Ptolemy
Return of the Flat Earth
By about 300AD, the idea of a Flat Earth was revived:
- Early Christian rejection of the "pagan absurdity" of a
spherical earth.
- This view was held sporadically until about 1300 AD.
By 1300, the works of Ptolemy and others arrived in Europe by way of
Islamic Spain, and fully restored the Spherical Earth to respectability.
Contrary to popular myth, very few educated people after about 300 BC
doubted that the Earth was a sphere. While a few early Christian
thinkers did try to reject the idea, there is nothing in Christian
beliefs that dictates a Flat Earth, in fact it says virtually nothing at
all on the matter.
Eratosthenes' work was lost, except for a description of his method in
an obscure source. [Note:The only description of
Erathosthenes' method that survives from antiquity is from On the
Orbits of the Heavenly Bodies written by Cleomedes in the 1st or
4th century AD (also known by the first word of its Greek title as the
Meteora). We know little or nothing else about Cleomedes,
not even his date or place of birth. It is clear that the numbers 5000
stadia and 1/50th of a circle have rounded off for convenience,
contributing to the inaccuracy of the final result.
However, while the derived circumference is off by ~15%, the actual
difference in latitude between Alexandria (31°13' N) and Syene/Aswan
(24°05' N) is 7°08', or about 0.0198 of the arc of a circle,
within 1% of the value 0.02 (1/50th) quoted by Cleomedes for
Eratosthenes. This is well within any measurement errors expected for
the time.]
Ptolemy's estimate survived in his influential writings on geography.
His estimate makes the eastern tip of Asia closer to the western
tip of Europe than it would be otherwise, which (interestingly!)
in part convinced Columbus that he might be able to reach Japan by sailing
West from the Canaries.
Unlike many others of his time, however, Columbus not only argued for a
smaller Earth, he also convinced the Spanish government to provide him
the means to put his claims to the test.
Updated: 2011 September 25, Todd A. Thompson
Copyright © Richard W. Pogge, All Rights Reserved.

